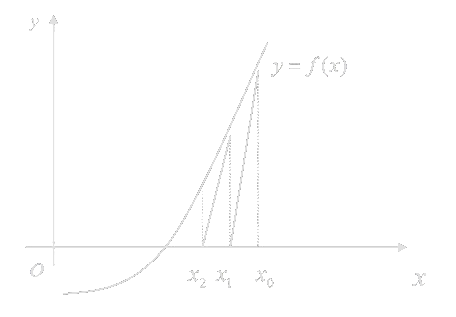缺点
- 在区间[a,b]的根多于一个时,二分法也只能找出一个。
- 若区间[a,b]内有重根时,也未必满足f(a)⋅f(b)<0。
迭代法构造思路:将Ax=b等价改写为x=Mx+g
仿照迭代法思路,将f(x)=0等价变换为x=φ(x)。
xk+1=φ(xk),k=0,1,2,⋯
- ∀x∈[a,b],有φ(x)∈[a,b]
- ∃L∈[0,1],∀x,y∈[a,b],有∣φ(x)−φ(y)∣≤L∣x−y∣
- ∃L∈[0,1], ∀x∈[a,b],有∣φ′(x)∣≤L<1
满足以上任意一条(2、3本质是一条),则可得到。
∀x0∈[a,b],由xk+1=φ(xk)得到的序列收敛于φ(x)在[a,b]上的唯一不动点。
简单迭代法的收敛性不但取决于迭代函数φ(x),还取决于x0。
事后估计
∣x∗−xk∣≤1−L1∣xk−xk−1∣
- 终止准则:1+∣xk∣∣xk−xk−1∣<ε
先验估计
∣x∗−xk∣≤1−LLk∣x1−x0∣
- 终止准则:k>lnLln(x1−x0(1−L)ε)
设x∗为方程x=φ(x)的根,φ′(x)在x∗的领域连续,且∣φ′(x∗)∣<1,则迭代过程xk+1=φ(xk)在根x∗领域具有局部收敛性。
设x∗是φ(x)的不动点,对于整数p>1,迭代函数φ(x)及其p阶导数在x∗的领域上连续,且满足:
φ′(x∗)=φ′′(x∗)=⋯=φ(p−1)(x∗)=0,φ(p)(x∗)=0
则迭代过程xk+1=φ(xk)在x∗的领域是 p阶收敛的,且有
k→∞lim(ek)pek+1=p!φ(p)(x∗)=C
- ek=∣x∗−xk∣:迭代误差
- C:渐进误差常数
也就是迭代过程的收敛速度依赖于迭代函数φ(x)的选取。
- p=1时,为线性收敛
- p=2时,为平方收敛
- p>1时,为超线性收敛
xk+1=xk+c(xk2−5),收敛到5(x∗=5)
- c的取值时,收敛(局部收敛性)
- c取何值时,满足平方收敛
- c取何值时,收敛最快
解
|
| φ(x)=x+c(x2−5) |
| φ′(x)=1+2cx |
| φ′′(x)=2c |
(1)
- ∣φ′(x∗)∣<1 ⇒ −55<c<0
(2)
- 明显φ′′(x)=0
- 当φ′(x∗)=0时,c=−105
- 故当c=−251,至少平方收敛到5
(3)
- 最高仅能保证平方收敛,故c=−251时收敛最快
艾特金(Aitken)
x^k+1=xk−xk+2−2xk+1+xk(xk+1−xk)2 k=0,1,2,⋯
该方法可以将一个线性收敛的序列{xk}转化为平方收敛的序列{x^k}。
斯蒂芬森(Steffensen)
把Aitken加速法的加速技巧与原迭代xk+1=φ(xk)相结合
⎩⎪⎪⎪⎨⎪⎪⎪⎧yk=φ(xk)zk=φ(yk)xk+1=xk−zk−2yk+xk(yk−xk)2k=0,1,2,⋯
亦可记作
xk+1=ψ(x) k=0,1,2,⋯
- ψ(x)=x−φ(φ(x))−φ(x)+x(φ(x)−x)2
说明
- 不论原迭代是否收敛,只要φ′(x∗)=1,则Steffensen方法至少是平方阶收敛的(p≥2)。
- 若原迭代是p阶收敛的,则Steffensen是p+1阶收敛的。
泰勒公式:f(x)=0!f(x0)+1!f′(x0)(x−x0)+2!f′′(x0)(x−x0)2+⋯+n!f(n)(x0)(x−x0)n+Rn(x)
取x0作为初始近似值,将f(x)在x0做一阶Taylor展开:
f(x)=f(x0)+f′(x0)(x−x0)+2!f′′(ξ)(x−x0)2
其中2!f′′(ξ)(x−x0)2是高阶小量,故只取前两项线性部分,利用线性方程来近似替代非线性方程。
0=f(x∗)≈f(x0)+f′(x0)(x∗−x0)
牛顿迭代公式
xk+1=xk−f′(xk)f(xk),k=0,1,⋯
几何意义
切线渐进
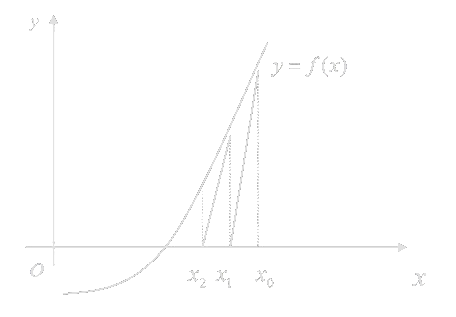
- 在单根附近,平方收敛
- 在重根附近,线性收敛
- 当已知根的重数m时,可构造xk+1=xk−mf′(xk)f(xk),此时可达局部平方收敛。
如果x0距离x∗比较远的话,可能导致牛顿是迭代法是发散的,为使得x0影响降到最低,使用牛顿下山法。
定义
满足∣f(xk+1)∣<∣f(xk)∣即具有单调性的牛顿迭代法,称为牛顿下山法。
构造思路
若由xk得到的xk+1不能使∣f∣减小,则再xk和xk+1之间找一个更好的点xk+1,使得∣f(xk+1)∣<∣f(xk)∣。
xk+1=λ[xk−f′(xk)f(xk)]+(1−λ)xk=xk−λf′(xk)f(xk)
当λ=1(此时就是牛顿迭代法)代入效果不好时,将λ减半计算。
xk+1=xk−Mf(x)k=0,1,2,⋯
其中M为常数。该方法只具有线性收敛。
xk+1=xk−f(xk)−f(xk−1)f(xk)(xk−xk−1),k=1,2,3,⋯
割线法收敛阶为p=21+5≈1.618。
xk+1=xk−f′(xk)2−f(xk)f′′(xk)f(xk)f′(xk),k=0,1,2,⋯
上式用于求方程f(x)=0重根的具有平方收敛的迭代法,且不需要知道根的重数。