数值分析：插值逼近

插值的定义

设函数y=f(x)y=f(x)在区间[a,b][a, b]上连续，给定n+1n+1个节点（a<x0<x1<⋯<xn<ba < x_0 < x_1 < \cdots < x_n < b，不一定均分），在函数类PP中寻找φ(x)φ(x)作为f(x)f(x)的近似表达，使其满足

φ(xk)=f(xk)=yk,   k=0,1,2,⋯ ,nφ(x_k)=f(x_k)=y_k, \,\,\, k=0,1,2,\cdots,n

被插值函数 插值函数 插值节点 插值区间 插值方法
y=f(x)y=f(x) φ(x)φ(x) x0<x1<⋯<xnx_0 < x_1 < \cdots < x_n [a,b][a,b] φ(xk)=f(xk)=ykφ(x_k)=f(x_k)=y_k

函数类PP的不同选取对应不同的插值方法。
满足插值条件的多项式Pn(x)P_n(x)存在且唯一。

拉格朗日（Lagrange）插值

线性插值

邻近的两点连成一条直线，即两点式L−f(x0)x−x0=f(x1)−f(x0)x1−x0\dfrac{L-f(x_0)}{x-x_0} = \dfrac{f(x_1)-f(x_0)}{x_1-x_0}

L2(x)=x−x0x1−x0[f(x1)−f(x0)]+f(x0)=x−x0x1−x0f(x1)+(1−x−x0x1−x0)f(x0)=x−x1x0−x1f(x0)+x−x0x1−x0f(x1)\begin{array}{l} L_2(x) \\ \\\\ \\\\ \\\\ \end{array} \begin{array}{l} = \dfrac{x-x_0}{x_1-x_0}\Big[f(x_1) - f(x_0)\Big] + f(x_0) \\\\ = \dfrac{x-x_0}{x_1-x_0}f(x_1) + (1-\dfrac{x-x_0}{x_1-x_0})f(x_0) \\\\ = \dfrac{x-x_1}{x_0-x_1}f(x_0) + \dfrac{x-x_0}{x_1-x_0}f(x_1) \end{array}

构造思路

图片来自互联网，故此处下标从1开始

假设已知(x1,y1)(x_1,y_1)、(x2,y2)(x_2,y_2)、(x3,y3)(x_3,y_3)，构造插值函数

L3(x)=y1f1(x)+y2f2(x)+y3f3(x)\begin{matrix} L_3(x) = y_1f_1(x) + y_2f_2(x) + y_3f_3(x) \end{matrix}

其中，fi(xj)={1i=j0i≠jf_i(x_j) = \begin{cases} 1 & i=j \\ 0 & i≠j \end{cases}，即选取一组线性无关的基然后确定坐标。

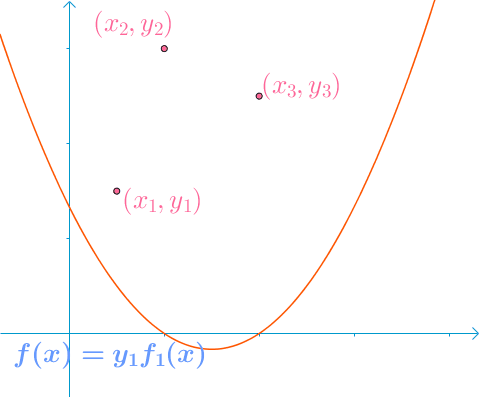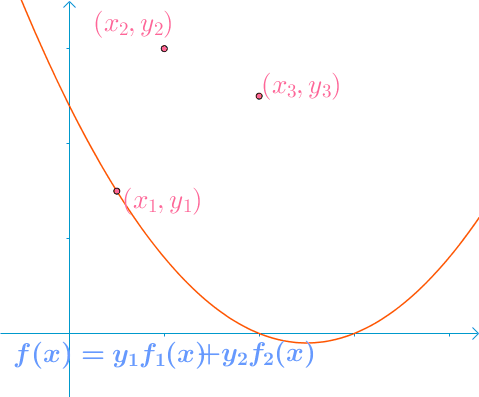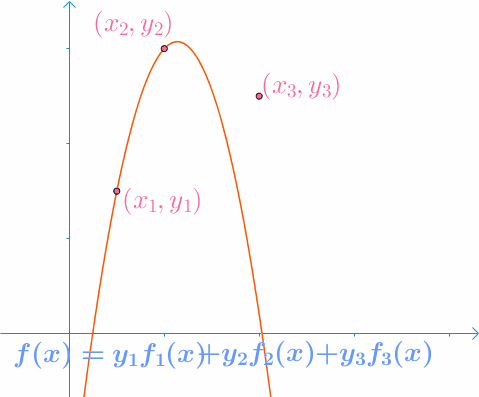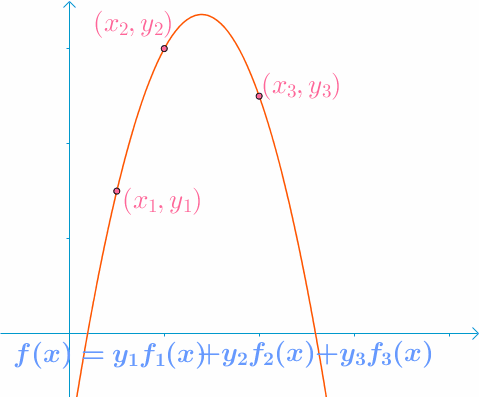
上面讨论中的fi(x)f_i(x)、yiy_i也就是接下来公式中的li(x)l_i(x)、f(xi)f(x_i)。该方法的缺陷是，当精度不够需要增加节点时，要重新确定基，即重新计算li(x)l_i(x)，而增加节点前的计算结果将毫无作用。

插值多项式

已知n+1n+1个坐标(x0,f(x0)),(x1,f(x1)),⋯ ,(xn,f(xn)){\big(x_0, f(x_0)\big)}, {\big(x_1, f(x_1)\big)},\cdots,{\big(x_n, f(x_n)\big)}构造构造nn次插值多项式

Ln(x)=∑i=0nli(x)f(xi)L_n(x) = \sum\limits_{i=0}^{n} l_i(x)f(x_i)

Ln(x)=∑i=0n[(∏j≠ij=0nx−xjxi−xj)f(xi)]L_n(x) = \sum\limits_{i=0}^{n} \left[ ( \prod\limits_{^{j=0}_{j≠i}}^{n} \dfrac{x-x_j}{x_i-x_j}) f(x_i) \right]

Ln(x)=∑i=0nωn+1(x)(x−xi)ωn+1′(xi)f(xi)L_n(x) = \sum\limits_{i=0}^{n} \dfrac{ ω_{n+1}(x) }{ (x-x_i)ω_{n+1}'(x_i) } f(x_i)

插值余项

Rn(x)=f(x)−Ln(x)=f(n+1)(ξ)(n+1)!ωn+1(x)ξ∈(a,b)=f(n+1)(ξ)(n+1)!∏i=0n(x−xi)ξ∈(a,b)\begin{array}{l} R_n(x) \\\\ \\\\ \\\\ \\ \end{array} \begin{array}{l} = f(x) - L_n(x) \\\\ = \dfrac{f^{(n+1)}(ξ)}{(n+1)!} ω_{n+1}(x) & ξ∈(a,b) \\\\ = \dfrac{f^{(n+1)}(ξ)}{(n+1)!} \prod\limits_{i=0}^{n} (x-x_i) & ξ∈(a,b) \end{array}

例

证明下述定理

由插值余项表达式，当xi,   i=0,1,2,…,nx_i, { \ \ \ } i=0,1,2,\dots,n为互异节点时

∑i=0nli(x)xik=xk   k=0,1,2,…,n\sum_{i=0}^{n} l_i(x)x_i^k = x^k { \ \ \ } k=0,1,2,\dots,n

解

取f(x)=xk   (k≤n)f(x) = x^k { \ \ \ } (k≤n)，有f(n+1)(x)=0f^{(n+1)}(x) = 0

则Rn(x)=xk−∑i=0nli(x)xik=0R_n(x) = x^k - \sum\limits_{i=0}^{n} l_i(x) x_i^k = 0

所以有xk=∑i=0nli(x)xikx^k =\sum\limits_{i=0}^{n} l_i(x) x_i^k

特别当k=0k=0时，∑i=0nli(x)=1\sum\limits_{i=0}^{n} l_i(x) = 1

截断误差限

插值余项表达式Rn(x)R_n(x)只在理论上说明ξξ存在，实际上f(n+1)(ξ)f^{(n+1)}(ξ)仍然依赖于xx（插值余项的大小与函数的n+1n+1阶导数的值有关）。因此Rn(x)R_n(x)的准确值是无法求出的，仅可用于截断误差估计。

由∣f(n+1)(ξ)∣≤Mn+1=max⁡a≤x≤b∣f(n+1)(x)∣|f^{(n+1)}(ξ)| ≤ M_{n+1} = \max\limits_{a≤x≤b} |f^{(n+1)}(x)|得

∣Rn(x)∣≤Mn+1(n+1)!∣ωn+1(x)∣=max⁡a≤x≤b∣f(n+1)(x)∣(n+1)!∣∏i=0n(x−xi)∣|R_n(x)| ≤ \dfrac{M_{n+1}}{(n+1)!}|ω_{n+1}(x)| = \dfrac{ \max\limits_{a≤x≤b} \left|f^{(n+1)}(x)\right| }{(n+1)!} \left| \prod\limits_{i=0}^{n} (x-x_i) \right|

nn 名称 表达式
n=1n=1 线性插值误差限 ∣R1(x)∣≤12M2∣(x−x0)(x−x1)∣\vert{R_1(x)}\vert ≤ \frac{1}{2} M_2 \vert{(x-x_0)(x-x_1)}\vert
n=2n=2 二次插值误差限 ∣R2(x)∣≤16M3∣(x−x0)(x−x1)(x−x2)∣\vert{R_2(x)}\vert ≤ \frac{1}{6} M_3 \vert{(x-x_0)(x-x_1)(x-x_2)}\vert

例

y=f(x)=esin⁡x+log⁡∣x+2∣y = f(x) = e^{\sin x} + \log |x+2|的函数值表为

kk 0 1 2 3 4 5
xkx_k 0.0 0.2 0.4 0.6 0.8 1
yky_k 1.693 147 2.008 236 2.351 591 2.714 330 3.078 628 3.418 389

分别用线性插值、二次插值f(0.354)f(0.354)

解

Ln(x)=∑i=0n[(∏j≠ij=0nx−xjxi−xj)f(xi)]L_n(x) = \sum\limits_{i=0}^{n} \left[ ( \prod\limits_{^{j=0}_{j≠i}}^{n} \dfrac{x-x_j}{x_i-x_j}) f(x_i) \right]

∣Rn(x)∣≤Mn+1(n+1)!∣ωn+1(x)∣=max⁡a≤x≤b∣f(n+1)(x)∣(n+1)!∣∏i=0n(x−xi)∣|R_n(x)| ≤ \dfrac{M_{n+1}}{(n+1)!}|ω_{n+1}(x)| = \dfrac{ \max\limits_{a≤x≤b} \left|f^{(n+1)}(x)\right| }{(n+1)!} \left| \prod\limits_{i=0}^{n} (x-x_i) \right|

 
（1）选取(0.2,2.008236)(0.2, 2.008 236)、(0.4,2.351591)(0.4, 2.351 591)，构造线性插值

L1(x)=x−0.40.2−0.42.008236+x−0.20.4−0.22.351591L_1(x) = \dfrac{x-0.4}{0.2-0.4}2.008 236 + \dfrac{x-0.2}{0.4-0.2}2.351 591

f1(0.354)≈L1(0.354)≈2.272619f_1(0.354) ≈ L_1(0.354) ≈ 2.272619

∣R1(x)∣≤max⁡0.2≤x≤0.4∣f′′(x)∣2∣(x−0.2)(x−0.4)∣|R_1(x)| ≤ \dfrac{\max\limits_{0.2≤x≤0.4} |f''(x)|}{2} \big|{(x-0.2)(x-0.4)}\big|

∣R1(0.354)∣≤0.7226902∣(0.354−0.2)(0.354−0.4)∣=0.002560|R_1(0.354)| ≤ \dfrac{0.722690}{2} \big|{(0.354-0.2)(0.354-0.4)}\big| = 0.002560

 
（2）选取(0.0,1.693147)(0.0, 1.693 147)、(0.2,2.008236)(0.2, 2.008 236)、(0.4,2.351591)(0.4, 2.351 591)，（也可选取(0.2,2.008236)(0.2, 2.008 236)、(0.4,2.351591)(0.4, 2.351 591)、(0.6,2.714330)(0.6, 2.714 330)），构造二次插值

L2(x)=x−0.20−0.2⋅x−0.40−0.4⋅1.693147+x−00.2−0⋅x−0.40.2−0.4⋅2.008236+x−00.4−0⋅x−0.20.4−0.2⋅2.351591L_2(x) = \dfrac{x-0.2}{0-0.2} \cdot \dfrac{x-0.4}{0-0.4} \cdot 1.693 147 + \dfrac{x-0}{0.2-0} \cdot \dfrac{x-0.4}{0.2-0.4} \cdot 2.008236 + \dfrac{x-0}{0.4-0} \cdot \dfrac{x-0.2}{0.4-0.2} \cdot 2.351591

∣R2(x)∣≤max⁡0.0≤x≤0.4∣f(3)(x)∣6∣(x−0.0)(x−0.2)(x−0.4)∣|R_2(x)| ≤ \dfrac{\max\limits_{0.0≤x≤0.4} |f^{(3)}(x)|}{6} \big|{(x-0.0)(x-0.2)(x-0.4)}\big|

计算略

事后误差估计

为解决插值余项表达式Rn(x)R_n(x)不可计算的问题，提出事后误差估计表达式。

利用插值节点x0,x1,⋯ ,xnx_0,x_1,\cdots,x_n得到插值多项式Ln(x)L_n(x)
利用插值节点x1,x2,⋯ ,xn+1x_1,x_2,\cdots,x_{n+1}得到插值多项式L~n(x)\tilde{L}_n(x)

得两组插值余项

认为f(n+1)(ξ)≈f(n+1)(η)f^{(n+1)}(ξ) ≈ f^{(n+1)}(η)则

Rn(x)R~n(x)=f(x)−Ln(x)f(x)−L~n(x)≈x−x0x−xn+1\dfrac{ R_n(x) }{ \tilde{R}_n(x) } = \dfrac{ f(x) - L_n(x) }{ f(x) - \tilde{L}_n(x) } ≈ \dfrac{ x - x_0 }{ x - x_{n+1} }

得事后误差估计表达式

Rn(x)=f(x)−Ln(x)≈x−x0x0−xn+1(Ln(x)−L~(x))R_n(x) = f(x) - L_n(x) ≈ \dfrac{x-x_0}{x_0-x_{n+1}} (L_n(x) - \tilde{L}(x))

牛顿（Newton）插值

插值多项式

Nn(x)=∑k=0nckωk(x)=f(x0)+   f[x0,x1](x−x0)+   f[x0,x1,x2](x−x0)(x−x1)+   ⋯+   f[x0,⋯ ,xn](x−x0)⋯(x−xn−1)\begin{array}{l} N_n(x) \\ \\\\ \\\\ \\\\ \end{array} \begin{array}{l} = \sum\limits_{k=0}^{n} c_k ω_k(x) \\ \\ = f(x_0) \\ + { \ \ \ } f[x_0,x_1](x-x_0) \\ + { \ \ \ } f[x_0,x_1,x_2](x-x_0)(x-x_1) \\ + { \ \ \ } \cdots \\ + { \ \ \ } f[x_0,\cdots,x_n](x-x_0)\cdots(x-x_{n-1}) \end{array}

牛顿插值多项式与拉格朗日插值多项式是等价的，它们只是形式不同，但表示的都是同一个多项式。

利用牛顿插值公式还可方便地导出某些带导数的插值公式。

插值余项

Rn(x)=f(x)−Nn(x)=f[x,x0,x1,⋯ ,xn]ωn+1(x)R_n(x) = f(x) - N_n(x) = f[x,x_0,x_1,\cdots,x_n]ω_{n+1}(x)

牛顿插值多项式插值余项与拉格朗日插值多项式插值余项是等价的。

故f[x,x0,⋯ ,xn]ωn+1(x)=f(n+1)(ξ)(n+1)!ωn+1(x)f[x,x_0,\cdots,x_n]ω_{n+1}(x) = \dfrac{f^{(n+1)}(ξ)}{(n+1)!} ω_{n+1}(x)，得f[x,x0,⋯ ,xn]=f(n+1)(ξ)(n+1)!f[x,x_0,\cdots,x_n] = \dfrac{f^{(n+1)}(ξ)}{(n+1)!}

与拉格朗日插值多项式插值余项相比牛顿插值多项式插值余项更具有一般性，其对ff离散或ff导数不存在均适用。

例

已知100=10\sqrt{100}=10、121=11\sqrt{121}=11、144=12\sqrt{144}=12，求115\sqrt{115}

解

记f(x)=xf(x) = \sqrt{x}

xx f(x)f(x) 一阶 二阶
100100 1010
121121 1111 11−10121−100=121\frac{11-10}{121-100}=\frac{1}{21}
144144 1212 12−11144−121=123\frac{12-11}{144-121}=\frac{1}{23} 123−121144−100\dfrac{\frac{1}{23}-\frac{1}{21}}{144-100}

N2(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)N_2(x) = f(x_0) + f[x_0,x_1](x-x_0) + f[x_0,x_1,x_2](x-x_0)(x-x_1)

则N2(115)=N_2(115) =（计算略）

埃尔米特（Hermite）插值

在插值节点上，不仅要求函数值相等，还要求导数值相等。

基于Lagrange插值基函数

略

基于Newton插值基函数

若差商f[x0,⋯ ,xn]f[x_0,\cdots,x_n]中存在重节点，由f[x0,⋯ ,xn]=f(n)(ξ)n!,   ξ∈[a,b]f[x_0,\cdots,x_n] = \dfrac{f^{(n)}(ξ)}{n!}, \,\,\, ξ∈[a,b]，定义一般重节点差商表达式：∀x∈Rn∀x∈R^n，

f[x,x,⋯ ,x⏟]n+1=lim⁡xi→x,i=0,1,⋯ ,nf[x0,x1,⋯ ,xn]=lim⁡ξ→xf(n)(ξ)n!=f(n)(x)n! \begin{matrix} f[\underbrace{x,x,\cdots,x}] \\ _{n+1} \end{matrix} \begin{matrix} = \lim\limits_{x_i→x, i=0,1,\cdots,n} f[x_0,x_1,\cdots,x_n] = \lim\limits_{ξ→x} \dfrac{ f^{(n)}(ξ) }{ n! } = \dfrac{ f^{(n)}(x) }{ n! } \\ \, \end{matrix}

考虑2n+22n+2个互异节点z0,z1,⋯ ,z2n+1z_0,z_1,\cdots,z_{2n+1}的Newton插值多项式

由差商连续性，当节点zz有重复时，上述公式仍然成立。

现令z2i=z2i+1=xi,   i=0,1,⋯ ,nz_{2i} = z_{2i+1} = x_i, \,\,\, i=0,1,\cdots,n，得：

N2n+1(x)=f(x0)+   f[x0,x0](x−x0)+   f[x0,x0,x1](x−x0)2+   ⋯+   f[x0,x0,⋯ ,xn,xn](x−x0)2⋯(x−xn−1)2(x−xn)\begin{matrix} N_{2n+1}(x) = \\ \\\\ \\\\ \end{matrix} \begin{array}{l} f(x_0) \\ + { \ \ \ } f[x_0,x_0](x-x_0) \\ + { \ \ \ } f[x_0,x_0,x_1](x-x_0)^2 \\ + { \ \ \ } \cdots \\ + { \ \ \ } f[x_0,x_0,\cdots,x_n,x_n](x-x_0)^2\cdots(x-x_{n-1})^2(x-x_n) \end{array}

误差为

R2n+1(x)=f[x,x0,x0,⋯ ,xn,xn]ωn+12(x)R_{2n+1}(x) = f[x,x_0,x_0,\cdots,x_n,x_n]ω^2_{n+1}(x)

N2n+1(x)N_{2n+1}(x)即为Newton形式Hermite插值多项式。

例1

函数f(x)f(x)满足f(−1)=−2f(-1)=-2，f(0)=−1f(0)=-1、f(1)=0f(1)=0、f′(0)=0f'(0)=0，求不超过3次的满足p3(−1)=f(−1)p_3(-1)=f(-1)、p3(0)=f(0)p_3(0)=f(0)、p3(1)=f(1)p_3(1)=f(1)、p3′(0)=f′(0)p'_3(0) = f'(0)的多项式p3(x)p_3(x)。

解

记x0,x1,x2=−1,0,1x_0,x_1,x_2 = -1,0,1，构造p3(x)p_3(x)

p3(x)=f(x0)+f[x0,x1](x−x0)+f[x0,x1,x2](x−x0)(x−x1)+λ(x−x0)(x−x1)(x−x2)p_3(x) = f(x_0) + f[x_0,x_1](x-x_0) + f[x_0,x_1,x_2](x-x_0)(x-x_1) + λ(x-x_0)(x-x_1)(x-x_2)

则p3(x)=−2+(x+1)+0+λ(x+1)x(x−1)=λ(x3−x)+x−1p_3(x) = -2 + (x+1) + 0 + λ(x+1)x(x-1) = λ(x^3-x) + x - 1

则p3′(x)=λ(3x2−1)+1p'_3(x) = λ(3x^2-1) + 1

p3′(0)=0   ⇒   −λ+1=0   ⇒   λ=1p'_3(0) = 0 { \ \ \ ⇒ \ \ \ } -λ + 1 = 0 { \ \ \ ⇒ \ \ \ } λ = 1

综上，解得p3(x)=x3−1p_3(x) = x^3 - 1

例2

求一个4次插值多项式H4(x)H_4(x)，使得

写出插值余项表达式。

答

记x0,x1=0,1x_0,x_1=0,1，明显x0x_0为2重节点；x1x_1为3重节点。

计算差商表得

xx H(x)H(x) 一阶 二阶 三阶 四阶
00 −1-1
00 −1-1 f[0,0]=f′(0)1!=H′(0)=−2f[0,0]=\dfrac{f'(0)}{1!}=H'(0)=-2
11 00 f[0,1]=1f[0,1]=1 f[0,0,1]=3f[0,0,1]=3
11 00 f[1,1]=f′(1)1!=H′(1)=10f[1,1]=\dfrac{f'(1)}{1!}=H'(1)=10 f[0,1,1]=9f[0,1,1]=9 f[0,0,1,1]=6f[0,0,1,1]=6
11 00 1010 f[1,1,1]=f′′(1)2!=H′′(1)2=20f[1,1,1]=\dfrac{f''(1)}{2!}=\dfrac{H''(1)}{2}=20 f[0,1,1,1]=11f[0,1,1,1]=11 f[0,0,1,1,1]=5f[0,0,1,1,1]=5

带入Newton插值公式N(x)N(x)得

H4(x)=−1−2x+3x2+6x2(x−1)+5x2(x−1)2H_4(x) = -1 -2x + 3x^2 + 6x^2(x-1) + 5x^2(x-1)^2

R4(x)=f(n+1)(ξ)(n+1)!∏i=0n(x−xi)=f(5)(ξ)5!x2(x−1)30<ξ<1R_4(x) = \dfrac{f^{(n+1)}(ξ)}{(n+1)!} \prod\limits_{i=0}^{n} (x-x_i) = \begin{matrix} \dfrac{f^{(5)}(ξ)}{5!}x^2(x-1)^3 & 0<ξ<1 \end{matrix}

分段插值

龙格（Runge）现象

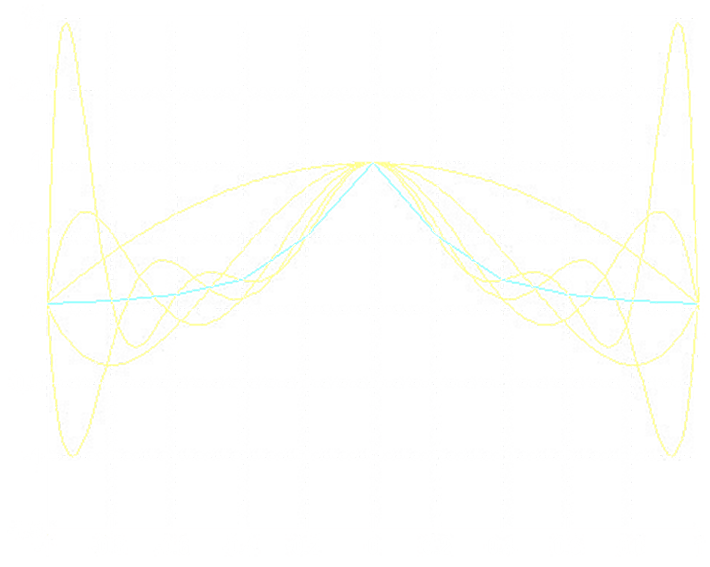
在区间两端，插值次数越高，插值结果与原函数偏离越大的现象。

分段线性插值

相邻两个插值节点做线性插值。但会导致不可导。

分段三次Hermite插值

只能保证一阶线性可导。

H3(i)(x)=φi−1(x)yi−1+φi(x)yi+ψi−1(x)yi−1′+ψi(x)yi′H_3^{(i)}(x) = φ_{i-1}(x)y_{i-1} + φ_{i}(x)y_{i} + ψ_{i-1}(x)y_{i-1}' + ψ_{i}(x)y_i'

φi−1(x)=1hi3(2x+xi−3xi−1)(x−xi)2φ_{i-1}(x) = \dfrac{1}{h_i^3} (2x+x_i-3x_{i-1})(x-x_i)^2
φi(x)=1hi3(3xi−2x−xi−1)(x−xi−1)2φ_{i}(x) = \dfrac{1}{h_i^3}(3x_i-2x-x_{i-1})(x-x_{i-1})^2
ψi−1(x)=1hi2(x−xi−1)(x−xi)2ψ_{i-1}(x) = \dfrac{1}{h_i^2}(x-x_{i-1})(x-x_i)^2
ψi(x)=1hi2(x−xi−1)2(x−xi)ψ_i(x) = \dfrac{1}{h_i^2}(x-x_{i-1})^2(x-x_i)

三次样条插值

若函数S(x)∈C2[a,b]S(x)∈C^2[a,b]，且在每个小区间[xj,xj+1][x_j, x_{j+1}]上是三次多项式，其中a=x0<x1<⋯<xn=ba = x_0 < x_1 < \cdots < x_n = b是给定节点，则称S(x)S(x)是节点x0,x1,⋯ ,xnx_0, x_1, \cdots, x_n上的三次样条函数，aj,bj,cj,dja_j,b_j,c_j,d_j为待定参数。

S(x)=ajx3+bjx2+cjx+dj,   j=0,1,2,⋯ ,n−1S(x) = a_jx^3 + b_jx^2 + c_jx + d_j, \,\,\, j=0,1,2,\cdots,n-1

边界条件

（1）已知两个端点的一阶导数值

（2）已知两个端点的二阶导数值

特别的，当S′′(x0)=S′′(xn)=0S''(x_0)=S''(x_n)=0时，称为自然边值条件。

（3）f(x)f(x)是以xnx_n—x0x_0为周期的函数

要求S(x)S(x)也是周期函数，此时边界条件满足：

此时称作周期样条函数。

三转角方法

直接利用三次分段Hermite插值

S(x)=∑j=0n[yjaj(x)+mjβj(x)]S(x) = \sum\limits_{j=0}^{n} [y_ja_j(x) + m_jβ_j(x)]

该方法对边界条件（1）的计算量最低。

三弯矩方法

S(x)=(xi−x)3Mi−1+(x−xi−1)3Mi6hi+(yi−1hi−hiMi−16)(xi−x)+(yihi−hiMi6)(x−xi−1)S(x) = \dfrac{ (x_i-x)^3M_{i-1} + (x-x_{i-1})^3M_i }{ 6h_i } + \left({ \dfrac{y_{i-1}}{h_i} - \dfrac{h_iM_{i-1}}{6} }\right) (x_i-x) + \left({ \dfrac{y_i}{h_i} - \dfrac{h_iM_i}{6} }\right) (x-x_{i-1})

该方法对边界条件（2）的计算量最低。