数据结构
线性表
顺序结构
typedef struct { ElemType* elements; // 存储位置 unsigned int size; // 已用长度 unsigned int capacity; // 最大容量 } ArrayList;
链表结构
单向链表:
typedef struct LinkedListNode { ElemType element; struct LinkedListNode* next; } LLNode; typedef struct { struct LinkedListNode* head; unsigned int size; // 链表长度 } LinkedList;
双向链表:
typedef struct DoubleLinkedListNode { ElemType element; struct DoubleLinkedListNode* next; struct DoubleLinkedListNode* prior; } DLLNode; typedef struct { struct DoubleLinkedListNode* head; struct DoubleLinkedListNode* tail; unsigned int size; // 链表长度 } DoubleLinkedList;
循环链表:

栈
先进后出
typedef struct { ElemType* base; ElemType* top; // default = base // int top; // default = -1 unsigned int capacity; } Stack; /** * 判空 */ bool isEmpty(Stack* S) { return (S->top) == (S->base); // return (S->top) == -1; } /** * 判满 */ bool isFull(Stack* S) { return (S->top) == ((S->base) + (S->capacity)); // return (S->top) == ((S->capacity) - 1); } /** * 数量 */ unsigned int size(Stack* S) { return (S->top) - (S->base); // return (S->top) + 1; } /** * 栈顶 */ ElemType size(Stack* S) { if ( (S->top) > (S->base) ) { return *((S->top) - 1); } return NULL; } /** * Push */ bool push(Stack* S, ElemType E) { if ( (S->top) < ((S->base) + (S->capacity)) ) { *(S->top)++ = E; return true; } return false; } /** * Pop */ ElemType pop(Stack* S) { if ( (S->top) > (S->base) ) { return *--(S->top); } return NULL; }
队列
先进先出
typedef struct { ElemType* base; unsigned int capacity; int front; int rear; } CircularQueue; /** * 判空 */ bool isEmpty(CircularQueue* Q) { return (Q->front) == (Q->rear); } /** * 判满 */ bool isFull(CircularQueue* Q) { return ((Q->rear) + 1) % (Q->capacity) == (Q->front); } /** * 数量 */ unsigned int size(CircularQueue* Q) { return ((Q->rear) - (Q->front) + (Q->capacity)) % (Q->capacity); } /** * 入队 */ bool enQueue(CircularQueue* S, ElemType E) { int nextRear = ((Q->rear) + 1) % (Q->capacity); if ( nextRear != (Q->front) ) { Q->base[Q->rear] = E; Q->rear = nextRear; return true; } return false; } /** * 出队 */ ElemType deQueue(CircularQueue* S) { if ( (Q->front) != (Q->rear) ) { ElemType e = Q->base[Q->front]; Q->front = ((Q->front) + 1) % (Q->capacity); return e; } return NULL; }
串
空串:""
字串:串中任意个连续字符组成的子序列。
串的表示
/** * 定长存储 * 第一个位置存储字符长度 */ typedef unsigned char SString[256];
/** * 堆分配存储 */ typedef struct { unsigned char* chs; unsigned int length; } HString;
/** * 块链存储 */ struct Chunk { unsigned char chs[32]; struct Chunk* next; }; typedef struct { struct Chunk* head; unsigned int length; } LString;
串的模式匹配
/** * 求子串位置 */ int indexOf(const char* mainStr, const char* findStr) { const int N = strlen(mainStr); const int M = strlen(findStr); int i = 0, j = 0; while (i < N && j < M) { if (mainStr[i] == findStr[j]) { i++; j++; } else { i = i - j + 1; j = 0; } } return j == M ? i - M : -1; } int main() { printf("%d=8\n", indexOf("Hello, world!", "or")); }
/** * KMP算法 */ // 待补充
树
表示方法
树形表示法、嵌套集合表示法、凹入表示法、广义表表示法
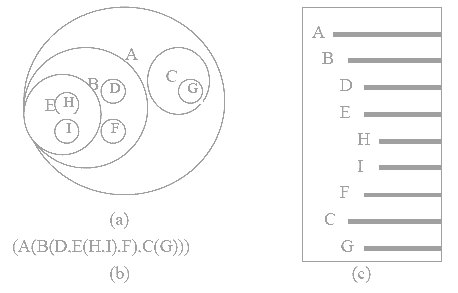
二叉树
- 第层至多有个节点
- 深度为的二叉树至多有个节点
- 终端节点数,度为的结点数,则
- 个结点的完全二叉树深度为
- 个结点的完全二叉树,从上到下,从左到右编号
- 为根节点
- 若,则结点无左子或左子是结点
- 若,则结点无右子或右子是结点
- 最后一个非叶节点为
存储结构
顺序存储、链式存储
/** * 顺序存储 */ int bt1[] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15};
/** * 链式存储 */ typedef struct BinaryTreeNode { int val; struct BinaryTreeNode* left; struct BinaryTreeNode* right; } BinaryTreeNode;
遍历
对一个非线性结构进行线性化操作。
void Traverse(BinaryTreeNode* root) { if(root) { printf("前序遍历:%d\n", root->val); Traverse(root->left); printf("中序遍历%d\n", root->val); Traverse(root->right); printf("后续遍历%d\n", root->val); } }
线索化
增加2个表示存储的是“前驱、后继、左子、右子”。
| lChild | lTag | data | rTag | rchild |
,
在有个结点的二叉链表中必定存在个空链域。
树和森林
树的表示法
双亲表示法、孩子表示法、孩子兄弟表示法
/** * 双亲表示法 */ struct ParentTreeNode { ElemType data; int parent; // Parent在数组中的下标 }; typedef struct { struct ParentTreeNode nodes[100]; int root; // 根在数组中的下标 int size; // 结点数 } ParentTree;
/** * 孩子表示法 */ struct ChildTreeNode { int child; // Child在数组中的下标 struct ChildTreeNode* next; }; typedef struct ChildTreeBox { ElemType data; struct ChildTreeNode* firstChild; }; typedef struct{ struct ChildTreeBox nodes[100];//存储结点的数组 int root; // 根在数组中的下标 int size; // 结点数 } ChildTree;
/** * 孩子兄弟表示法 */ typedef struct ChildSiblingTreeNode { ElemType data; struct ChildSiblingTreeNode* firstChild; struct ChildSiblingTreeNode* nextSibling; } CSNode, *CSTree;
转化为二叉树
树转换为二叉树:
- 同层相连
- 每层与上层仅保留最左侧链接
森林转为二叉树:
- 将每颗树转为二叉树
- 第二颗树作为第一颗的右子树,依次类推
Huffman
带权路径长度:从树根到某一节点的路径长度与该节点的权的乘积。
构建:选出最小的两个作为左右子树,构建出一颗新二叉树,其根为两数之和;新根元素替代原有两个元素参与后续构建,重复上述步骤直到不能凑齐两个元素。
编码:每条路径权值为0或1(一般左0右1),每个元素编码为从根到该元素所有路径的权值组成的数字。
图
图的表示法
邻接矩阵、邻接表、十字链表、邻接多重表
/** * 邻接矩阵 */ enum GraphKind{ DG, DN, UDG, UDN }; // 有向图, 有向网, 无向图, 无向网 struct VexNode { ElemType data; // 顶点信息 }; struct ArcCell { InoType info; // 弧的信息 }; typedef struct { struct VexNode vexs[MAX_VERTEX_NUM]; // 顶点向量 struct ArcCell arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 邻接矩阵 int vexnum; // 顶点数 int arcnum; // 弧数量 enum GraphKind kind; // 图的种类 } MGraph;
/** * 邻接表 */ struct ArcCell { int adjvex; // 弧所指向顶点位置 struct ArcCell* next; // 下一条弧 InoType info; // 弧所含信息 }; struct VexNode { ElemType data; struct ArcCell* first; // 该节点所有的弧 }; typedef struct { struct VexNode vexs[MAX_VERTEX_NUM]; int vexnum; // 顶点数 int arcnum; // 弧数量 enum GraphKind kind; // 图的种类 } ALGraph;
图的遍历
/** * DFS */ // 待补充
/** * BFS */ // 待补充
图的连通性
连通图(无向图):任意两点有路径。
连通分量(无向图):图的连通子图,连通图的连通分量只有自身。
强连通图(有向图):任意两点可以互相到达。
强连通分量(有向图):有向图的强连通子图,强连通图的强连通分量只有自身。
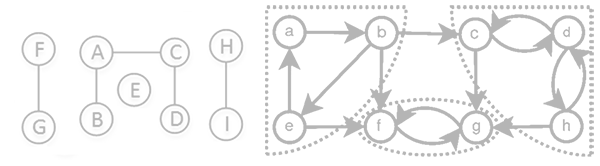
最小生成树
构造联通网的最小代价生成树。
Prim:
- 任取一个点作为已够部分;
- 将剩余点看成一个整体;
- 连接“剩余”与“已构”代价最小的一条边;
- 重复上述步骤直到构成一个完整的整体。
7、3、3、2、2
Kruskal:
- 画出所有顶点;
- 从边集中选出未用未排除的最小的一条加入;
- 若该边不能连通新的两棵树,则换选次小或同权其它的边;
- 重复上述步骤,直到选出条边停止。
2、2、3、3、7
有向无环图(DAG)
拓扑排序——AOV网
拓扑排序通常用来“排序”具有依赖关系的任务。
- 从有向图中找到一个没有前驱的点(入度为0)并输出,拿掉以该点为起点的所有边;
- 重复上述步骤,直到没有元素,或没有入度为0的点(此时必定有环)。
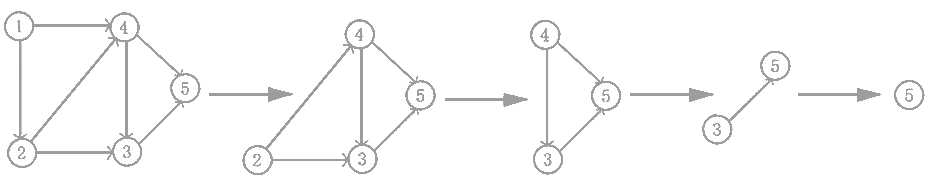
1、2、4、3、5
关键路径——AOE网
解决工程完成需要最短时间问题。
源点:入度为0的点。
汇点:出度为0的点。
关键路径:从源点到汇点最大长度的路径。
:活动最早开始时间。
:活动最晚开始时间。
:事件最早发生时间。
:事件最晚发生时间。
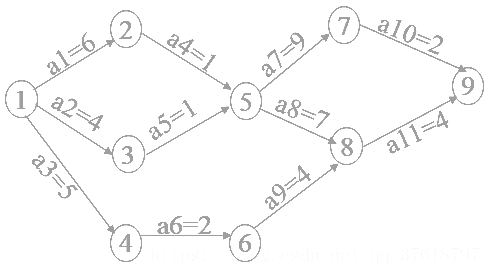
| 顶点 | |||
|---|---|---|---|
| 或 |
最短路径
Dijkstra:
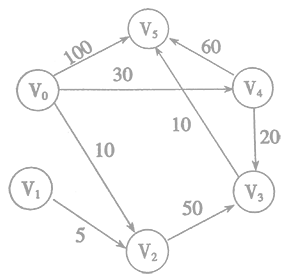
| 终点 | 直达 | 加入 | 加入 | 加入 | 加入 | 最短路径 |
|---|---|---|---|---|---|---|
| 0 |
Floyd:
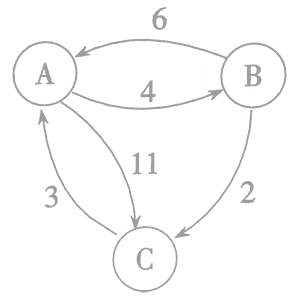
加入,有B->A->C = 17、C->A->B = 7
加入,有A->B->C = 6
加入,有B->C->A = 5
动态存储
分配方法
- 首次拟合
- 最佳拟合
- 最差拟合
边界标识
- 可利用空间表结构
- 分配算法
- 回收算法

伙伴协同
无论占用块还是空闲块,其大小均为大小
查找
查找方法
顺序查找、折半查找、分块查找
/** * 折半查找 */ int binarySearch(const int A[], const int N, const int K) { int l = 0, r = N - 1; while (l <= r) { int m = (l + r) / 2; if (A[m] == K) { return m; } else if (A[m] < K) { l = m + 1; } else if (A[m] > K) { r = m - 1; } } return -1; }
查找结构
平衡二叉树(AVL)
//! 左单旋转 #define RR rotateLeft /*.........................................→.........................................* *....................A....................→....................C....................* *.................../.\...................→.................../.\...................* *................../...\..................→................../...\..................* *................./.....\.................→................./.....\.................* *................/.......\................→................/.......\................* *.............../.........\...............→.............../.........\...............* *............../...........\..............→............../...........\..............* *............./.............\.............→............./.............\.............* *............B..............(C)...........→............A...............G............* *.........................../.\...........→.........../.\............./.............* *........................../...\..........→........../...\.........../..............* *........................./.....\.........→........./.....\........./...............* *........................F.......G........→........B.......F.......N................* *.............................../.........→.........................................* *.............................[N].........→.........................................* *.........................................→.........................................*/ //! 右单旋转 #define LL rotateRight /*.........................................→.........................................* *....................A....................→....................B....................* *.................../.\...................→.................../.\...................* *................../...\..................→................../...\..................* *................./.....\.................→................./.....\.................* *................/.......\................→................/.......\................* *.............../.........\...............→.............../.........\...............* *............../...........\..............→............../...........\..............* *............./.............\.............→............./.............\.............* *...........(B)..............C............→............D...............A............* *.........../.\...........................→.........../.............../.\...........* *........../...\..........................→........../.............../...\..........* *........./.....\.........................→........./.............../.....\.........* *........D.......E........................→........H...............E.......C........* *......./.................................→.........................................* *.....[H].................................→.........................................* *.........................................→.........................................*/ //! 左右双旋 #define LR(t, n) rotateLeft(t, n); rotateRight(t, n) /*.........................................→.........................................→.........................................* *....................A....................→....................A....................→....................E....................* *.................../.\...................→.................../.\...................→.................../.\...................* *................../...\..................→................../...\..................→................../...\..................* *................./.....\.................→................./.....\.................→................./.....\.................* *................/.......\................→................/.......\................→................/.......\................* *.............../.........\...............→.............../.........\...............→.............../.........\...............* *............../...........\..............→............../...........\..............→............../...........\..............* *............./.............\.............→............./.............\.............→............./.............\.............* *............B...............C............→...........(E)..............C............→............B...............A............* *.........../.\...........................→.........../.\...........................→.........../.............../.\...........* *........../...\..........................→........../...\..........................→........../.............../...\..........* *........./.....\.........................→........./.....\.........................→........./.............../.....\.........* *........D......(E).......................→........B.......K........................→........D...............K.......C........* *.................\.......................→......./.................................→.........................................* *.................[K].....................→.....[D].................................→.........................................* *.........................................→.........................................→.........................................*/ //! 右左双旋 #define RL(t, n) rotateRight(t, n); rotateLeft(t, n) /*.........................................→.........................................→.........................................* *....................A....................→....................A....................→....................F....................* *.................../.\...................→.................../.\...................→.................../.\...................* *................../...\..................→................../...\..................→................../...\..................* *................./.....\.................→................./.....\.................→................./.....\.................* *................/.......\................→................/.......\................→................/.......\................* *.............../.........\...............→.............../.........\...............→.............../.........\...............* *............../...........\..............→............../...........\..............→............../...........\..............* *............./.............\.............→............./.............\.............→............./.............\.............* *............B...............C............→............B..............(F)...........→............A...............C............* *.........................../.\...........→.........................../.\...........→.........../.\...............\...........* *........................../...\..........→........................../...\..........→........../...\...............\..........* *........................./.....\.........→........................./.....\.........→........./.....\...............\.........* *.......................(F)......G........→........................L.......C........→........B.......L...............G........* *......................./.................→.................................\.......→.........................................* *.....................[L].................→.................................[G].....→.........................................* *.........................................→.........................................→.........................................*/ //■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■■ #define GetParent(n) (n->parent) #define BindRoot(t, n) t->root = n; if(n) n->parent = NULL #define BindLeft(n, nl) n->left = nl; if(nl) nl->parent = n #define BindRight(n, nr) n->right = nr; if(nr) nr->parent = n static void rotateLeft(struct RBTree* tree, struct RBTNode* node) { struct RBTNode* childR = node->right; struct RBTNode* parent = GetParent(node); if( NULL == parent ) { BindRoot(tree, childR); } else { if(parent->left == node) { BindLeft(parent, childR); } else { BindRight(parent, childR); } } BindRight(node, childR->left); BindLeft(childR, node); } static void rotateRight(struct RBTree* tree, struct RBTNode* node) { struct RBTNode* childL = node->left; struct RBTNode* parent = GetParent(node); if( NULL == parent ) { BindRoot(tree, childL); } else { if(parent->left == node) { BindLeft(parent, childL); } else { BindRight(parent, childL); } } BindLeft(node, childL->right); BindRight(childL, node); }
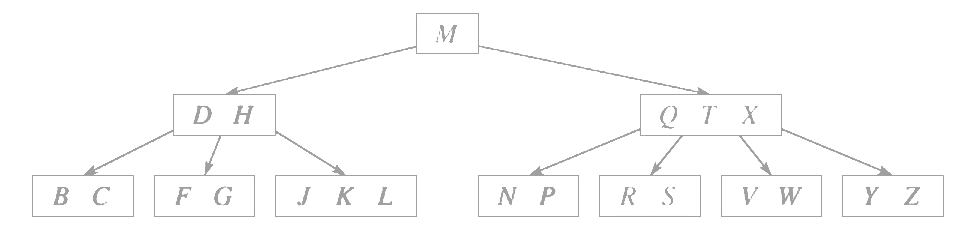
B树
- 每个结点最多有棵子树
- 若根不是叶子,则根至少有棵子树
- 除根结点外,所有非叶子结点至少有棵子树
- 所有叶子结点位于同一层次
- 所有非叶结点包含信息
typedef struct BTreeNode { int num; // 该结点关键字个数 KeyType key[EACH_KEY_SIZE]; // 关键字信息 struct BTreeNode *children[EACH_KEY_SIZE]; struct BTreeNode *parent; } BTreeNode, *BTree;
Hash表
构造方法:直接定址、数字分析、平方取中、折叠、除留余数。
处理冲突方法:开放地址、再Hash、溢出区、链地址