内排序

• 内排序
  • 插入排序
    • 直接插入排序
    • 折半插入排序
    • 希尔排序
  • 选择排序
    • 简单选择排序
    • 堆排序
      • ArrayToHeap
      • HeapAdjust
  • 交换排序
    • 冒泡排序
    • 快速排序
      • ArrayAdjustR
      • ArrayAdjustL
    • 快速排序三平均
  • 归并排序
  • 基数排序

插入排序

直接插入排序

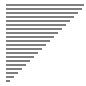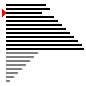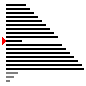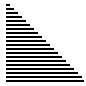
算法	完全随机	基本有序	逆排序	少有不同
插入排序

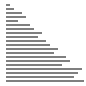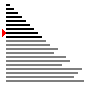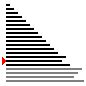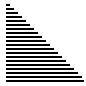
• 稳定
• 空间复杂度：$O(1)$
• 时间复杂度：$O(n^2)$
  • 序列完全正序：仅需比较$n-1$次
  • 序列完全逆序：比较$\sum\limits_{i=2}^{n}(i)$次、移动$\sum\limits_{i=2}^{n}(i+1)$次
  • 序列基本有序：$O(n)$
• 适应性：随着排序的的进行，序列变得基本有序，算法效率逐渐提高。

//! 直接插入排序（升序）
void directInsertSort(int arr[], int len) {
    for (int i = 1; i < len; i++) {
        int j = i - 1;
        int v = arr[i];
        while (j >= 0 && v < arr[j]) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = v;
    }
}

输入 A, N
循环 i ∈ [1, N - 1]
    j = i - 1, v = A[i]
    循环当 j ≥ 0 且 v < A[j]
        A[j + 1] = A[j]
        j--
    A[j + 1] = v

折半插入排序

//! 折半插入排序（升序）
void binaryInsertSort(int arr[], int len) {
    for (int i = 1; i < len; i++) {
        int l = 0, m, r = i - 1, v = arr[i];
        // 二分查找探测右边界
        while (l <= r) {
            m = (l + r) / 2;
            if (arr[m] <= v) {
                l = m + 1;
            } else {
                r = m - 1;
            }
        } // 插入位置为(r+1)
        int j = i - 1;
        while (j > r) {
            arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = v;
    }
}

输入 A, N
循环 i ∈ [1, N-1]
    l = 0, r = i - 1, v = A[i]
    循环当 l ≤ r
        m = (l + r) / 2
        若 A[m] <= v 则 l = m + 1 否则 r = m - 1
    j = i - 1
    循环当 j > r
        A[j + 1] = A[j]
        j--
    A[j + 1] = v

希尔排序

算法	完全随机	基本有序	逆排序	少有不同
希尔排序

• 不稳定
• 空间复杂度：$O(1)$
• 大概时间复杂度：$O(n^{\frac{3}{2}})$（由于数学问题，无法准确描述）
• 适应性：由于希尔排序基于插入排序，希尔排序继承了插入排序的自适应性，但适应性较直接插入排序弱。

//! 希尔排序（升序）
void shellInsertionSort(int arr[], int len) {
    for (int step = len / 2; step > 0; step /= 2) {
        for (int i = step; i < len; i++) {
            int j = i,
                k = j - step,
                dump = arr[j];
            // 直接插入排序
            while (k >= 0 && arr[k] > dump) {
                arr[j] = arr[k];
                j = k;
                k = j - step;
            }
            arr[j] = dump;
        }
    }
}

选择排序

简单选择排序

在交换单位的消耗成本很高的应用中，选择排序很可能也是合适的算法选择。

算法	完全随机	基本有序	逆排序	少有不同
选择排序

• 不稳定
• 空间复杂度：$O(1)$
• 时间复杂度：$O(n^2)$
• 不适应性

//! 简单选择排序（升序）
void simpleSelectSort(int arr[], int len) {
    for (int i = 0; i < len; i++) {
        // 获取[i, len - 1]中的最小值
        int m = i;
        for (int j = i + 1; j < len; j++) {
            if (arr[j] < arr[m]) m = j;
        }
        swapValue(arr, m, i);
    }
}

输入 A, N
循环 i ∈ [0, N - 1]
    m = i
    循环 j ∈ [i + 1, N - 1]
        若 A[j] < A[m] 则 m = j
    交换 A[i], A[m] 的值

堆排序

算法	完全随机	基本有序	逆排序	少有不同
堆排序

• 不稳定
• 空间复杂度：$O(1)$
• 时间复杂度：$O(n \cdot \log_{2}n)$
• 没有真正适应

//! 构建大顶堆
void heapAdjust(int arr[], int len, int i) {
    // i为被调整节点
    int iL = 2 * i + 1; // i 的左子节点
    int iR = 2 * i + 2; // i 的右子节点

    // 选出当前结点与其子结点中最大的结点记为j
    int j = i;
    if (iL < len && arr[iL] > arr[j]) j = iL;
    if (iR < len && arr[iR] > arr[j]) j = iR;

    // 最大结点交换到当前根，并传递调整
    if (j != i) {
        swapValue(arr, j, i);
        heapAdjust(arr, len, j);
    }
}

//! 堆排序（升序）
void heapSelectSort(int arr[], int len) {
    // 【构建大顶堆】
    // 所有非叶节点：[0, len / 2 - 1]
    for (int i = len / 2 - 1; i >= 0; i--) heapAdjust(arr, len, i);
    // 【调整大顶堆】
    for (int i = len - 1; i >= 1; i--) {
        swapValue(arr, i, 0);  // 将当前最大的放置到数组末尾
        heapAdjust(arr, i, 0); // 将未完成排序的部分继续进行堆排序
    }
}

输入 A, N
循环 i ∈ [N/2 - 1, 0]
    heapAdjust(A, N, i)
循环 i ∈ [N - 1, 1]
    交换 A[i], A[0] 的值
    heapAdjust(A, i, 0)

heapAdjust:
    输入 A, N, I
    l = 2 × I + 1
    r = 2 × I + 2

    j = I
    若 l < N 且 A[l] > A[j] 则 j = l
    若 r < N 且 A[r] > A[j] 则 j = r

    若 j ≠ I 则
        交换 A[j], A[I] 的值
        heapAdjust(A, N, j)

ArrayToHeap

• $\textnormal{\footnotesize 左子序} = \textnormal{\footnotesize 父序} × 2 + 1$
• $\textnormal{\footnotesize 右子序} = \textnormal{\footnotesize 父序} × 2 + 2$
• 非叶序区间：$\big[0, L / 2 - 1]$
• 叶子序区间：$\big[L / 2, L - 1\big]$

int A[] = {?, ?, ?, ?, ?, ?, ?, ?};
//    I = {0, 1, 2, 3, 4, 5, 6, 7};
//    L = 8;

HeapAdjust

int A[] = {49, 38, 13, 49, 76, 65, 27, 97};
// 构建大顶堆后
int R[] = {97, 76, 65, 49, 49, 13, 27, 38};

• 当前调整节点、被传递调整的节点、栈顶最值、取代栈顶的元素、冻结

• 0-4为构建大顶堆（需要从最后一个非叶结点到根结点进行HeapAdjust）；
• 4为构建大顶堆的结果；
• 从4开始为选择最大值排序，后续每次仅需对根节点进行HeapAdjust即可。

交换排序

冒泡排序

算法	完全随机	基本有序	逆排序	少有不同
冒泡排序

• 稳定
• 空间复杂度：$O(1)$
• 时间复杂的：$O(n^2)$
  • 基本有序：$O(n)$
• 适应性

//! 冒泡排序（升序）
void bubbleSwapSort(int arr[], int len) {
    // [0 →i→ (len-1)]
    for (int i = 0; i < len; i++) {
        // [(i+1) ←j← (len-1)] 每次从[i, len-1]中冒泡出一个最小值保存到i的位置
        for (int j = len - 1; j > i; j--) {
            if (arr[j - 1] > arr[j]) {
                swapValue(arr, j - 1, j);
            }
        }
    }
}

输入 A, N
循环 i ∈ [0, N - 1]
    循环 j ∈ [N - 1, i)
        若 A[j - 1] > A[j] 则 交换 A[j - 1], A[j] 的值

快速排序

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小。

算法	完全随机	基本有序	逆排序	少有不同
快速排序

• 不稳定
• 空间复杂度：$O(\log_{2}n)$
• 时间复杂度：$O(n^2)$，但通常$O(n \cdot log_{2}n)$
• 没有真正适应

static void arrayAdjustL(int arr[], int boundL, int boundR) {
    int l = boundL;
    int r = boundR;
    int v = arr[l];
    while (l < r) {
        // 期望右侧数据大于等于中间数
        while (l < r && arr[r] >= v) r--;
        arr[l] = arr[r];
        // 期望左侧数据小于等于中间数
        while (l < r && arr[l] <= v) l++;
        arr[r] = arr[l];
    }
    arr[l] = v;
    if (boundL < (l - 1)) arrayAdjustL(arr, boundL, l - 1);
    if ((l + 1) < boundR) arrayAdjustL(arr, l + 1, boundR);
}

//! 快速排序（升序）
void quickSwapSort(int arr[], int len) {
    if (len > 1) arrayAdjustL(arr, 0, len - 1);
}

输入 A, N
若 N > 1 则 arrayAdjust(A, 0, N - 1)

arrayAdjust:
    输入 A, L, R
    l = L, r = R, v = A[l]
    循环当 l < r
        循环当 l < r 且 A[r] ≥ A[p]
            r--
        A[l] = A[r]
        循环当 l < r 且 A[l] ≤ A[p]
            l++
        A[r] = A[l]
    A[l] = v
    若 L < (l - 1) 则 arrayAdjust(A, L, l - 1)
    若 (l + 1) < R 则 arrayAdjust(A, l + 1, R)

ArrayAdjustR

• $left$、$right$、$pivot$、临时锁定、最终命中、锁定

• 注意在5中，如果$pivot$是大于最终命中值的话是不需要交换的，此时锁定的是其原始所在位置。

ArrayAdjustL

• $left$、$right$、$pivot$、临时锁定、最终命中、锁定

快速排序三平均

算法	完全随机	基本有序	逆排序	少有不同
快速排序三平均

• 不稳定
• 空间复杂度：$O(\log_{2}n)$
• 时间复杂度：$O(n^2)$，但通常$O(n \cdot log_{2}n)$
• 自适应：当有$O(1)$个Unique Keys时需要$O(n)$时间

归并排序

算法	完全随机	基本有序	逆排序	少有不同
归并排序

• 稳定性
• 数组要$O(n)$额外空间；链表要$O(\log_{2}n)$额外空间
• $O(n \cdot \log_{2}n)$时间
• 不自适应
• 不需要随机接入数据

基数排序

略