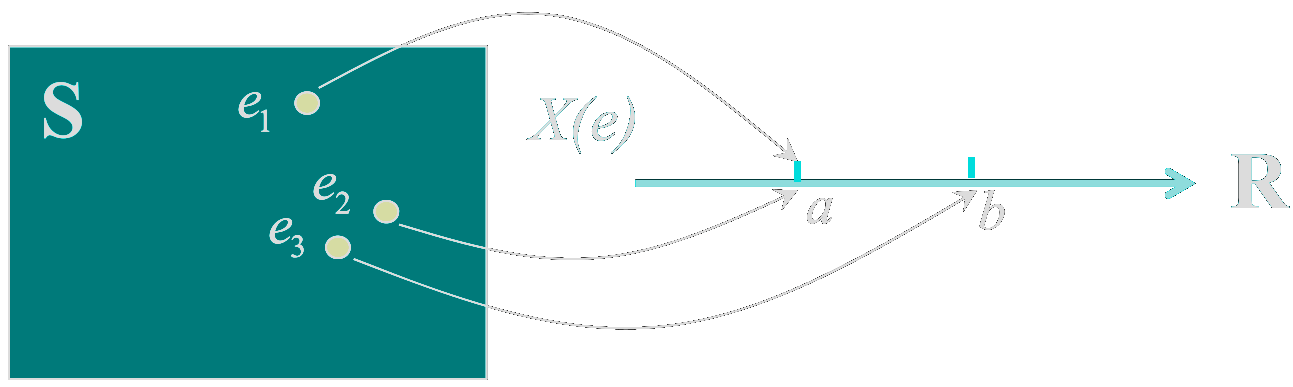
X(e)为定义在S上的实值单值函数,则称X(e)为随机变量。
- 对于i=j,必有X(i)∩X(j)=∅
概率密度函数对区间积分的面积就是事件在这个区间发生的概率。
∫−∞+∞f(t)dt=1
随机变量X的取值为有限个或可列无穷个。
P{X=xi}=pi, (i=1,2,…,n)
| X |
x1 |
x2 |
… |
xn |
| P |
p1 |
p2 |
… |
pn |
i=1∑npi=1
若它的样本空间只包含两个元素,我们总能在S={e1,e2}上定义一个服从伯努力分布分布的随机变量。
X={01e=e1e=e2
记为
X∼B(1,p):P{X=k}=pk(1−p)1−k,(k=0,1,…;0<p<1)
| X |
0 |
1 |
| P |
1−p |
p |
X∼B(n,p):P{X=k}=Cnkpk(1−p)n−k,(k=0,1,…;0<p<1)
X∼P(λ):P{X=k}=k!λke−λ,(k=0,1,2,…;λ>0)
X∼Geom(p):P{X=k}=pk−1(1−p),(k=1,2,…;0<p<1)
X H(n,M,N):P{X=k}=CNnCMkCN−Mn−k,(k=0,1,2,…,min(n,M))
X∼Unif(a,b)
密度函数:f(x)=⎩⎪⎨⎪⎧b−a1 0 a<x<bothers
分布函数:F(x)=⎩⎪⎪⎪⎨⎪⎪⎪⎧0b−ax−a1x<aa≤x≤bx>b
X∼Exp(λ)
密度函数:f(x)={λe−λx 0 x>0x≤0
分布函数:F(x)={1−e−λx 0 x>0x≤0
X∼N(μ,σ2)
密度函数:f(x)=2πσ1e−2σ2(x−μ)2 −∞<x<+∞
X∼N(0,1)
标准正态分布的密度函数:φ(x)=2π1e−2x2
标准正态分布的分布函数:Φ(x)=∫−∞x2π1e−2t2dt
密度函数:f(x)=⎩⎪⎨⎪⎧(n−1)!λnxn−1e−λx 0 x>0x≤0
密度函数:f(x)=⎩⎪⎨⎪⎧22nΓ(2n)1x2n−1e−2x 0 x>0x≤0
X∼Γ(r,λ)
Γ函数:Γ(r)=∫0+∞xr−1e−xdx, x∈(0,+∞)
密度函数:f(x)=⎩⎪⎨⎪⎧Γ(r)λrxr−1e−λx 0 x>0x≤0
当r=1,Γ(1)=1得到指数分布;
当r=n,Γ(n)=(n−1)!得到埃尔朗分布;
当r=2n,λ=21得到卡方分布;
