非线性规划：约束极值问题

• 非线性规划：约束极值问题
  • 最优性条件
    • 可行下降方向
    • 问题分类
    • K-T条件
      • 例
  • 制约函数法
    • 外点法（惩罚函数）
      • 例
    • 内点法（障碍函数）
      • 例

大多数极值问题其变量的取值都会受到一定限制，这种限制由约束条件（$h_i$、$g_j$）来体现。
$\begin{cases} \min f(x) \\ h_i(x) = 0, i=1,2,\cdots,m \\ g_j(x) ≥ 0, j=1,2,\cdots,l \end{cases}$ 或 $\begin{cases} \min f(x) & x∈R⊂E^n \\ R = \{ x | g_j(x) ≥ 0, j=1,2,\cdots,l \} \end{cases}$

最优性条件

可行下降方向

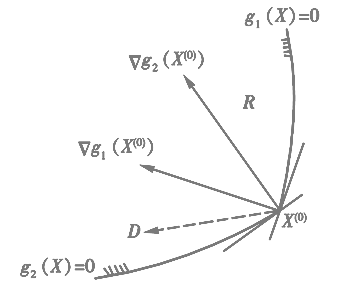
如果方向$D$既是$x^{(0)}$点的可行方向（约束范围内的方向），又是这个点的下降方向（和梯度方向成钝角的方向），就称它是该点的可行下降方向。该点存在可行下降方向与该点为极小点为互逆事件。

问题分类

假定$x^*$是非线性规划的极小点，则有以下两种情况：

• 极小点位于可行域的内部，即为无约束问题，$x^*$必满足$f(x^*) = 0$
• 极小点位于可行域的边界上，即为约束问题

K-T条件

库恩－塔克（Kuhn－Tucker）条件是确定某点为最优点的必要条件。

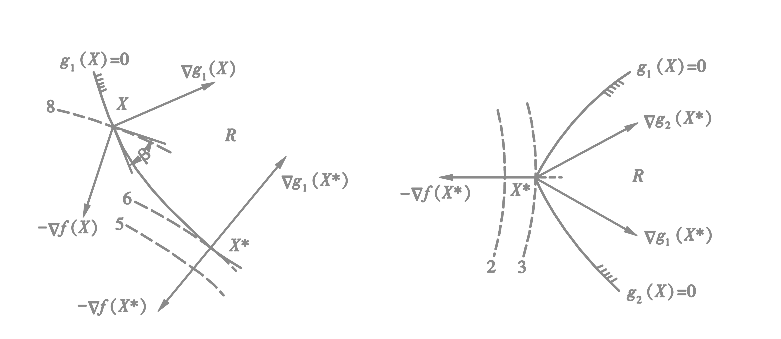
设$x^*$位于第一个约束条件形成的可行域边界上，即$g_1(x^*)=0$，若$x^*$是极小点，则$▽g_1(x^*)$与$▽f(x^*)$在一条直线上且方向相反。

$▽f(x^*) - γ_1▽g_1(x^*) = 0$

若$x^*$有两个起作用的约束$g_1(x^*)=0$、$g_2(x^*)=0$，则$▽f(x^*)$必处于$▽g_1(x^*)$与$▽g_2(x^*)$的夹角之内。

$▽f(x^*) - γ_1▽g_1(x^*) - γ_2▽g_2(x^*) = 0$

以此类推得

$\begin{cases} ▽f(x^*) - \sum\limits_{j=1}^{l} γ_j^* ▽g_j(x^*) = 0 \\ γ_j^*▽g_j(x^*) = 0 & j=1,2,\cdots,l \\ γ_j^* ≥ 0 & j=1,2,\cdots,l \end{cases}$

满足该条件的点，称为库恩-塔克（K-T）点。

例

用K-T条件解非线性规划$\begin{cases} \min f(x) = (x-3)^2 \\ 0≤x≤5 \end{cases}$

解

改写为$\begin{cases} \min f(x) = (x-3)^2 \\ g_1(x)=x≥0 \\ g_2(x)=5-x≥0 \end{cases}$

计算出梯度$\begin{cases} ▽f(x)=2(x-3) \\ ▽g_1(x)=1 \\ ▽g_2(x)=-1 \end{cases}$

设K-T点为$x^*$，该问题的K-T条件为$\begin{cases} 2(x^*-3) - γ_1^* - (-γ_2^*) = 0 \\ γ_1^*x^* = 0 \\ γ_2^*(5-x^*) = 0 \\ γ_1^*,γ_2^* ≥ 0 \end{cases}$

讨论

1. $γ_1^*≠0$、$γ_2^*≠0$：$x^*=0$与$x^*=5$矛盾，无解
2. $γ_1^*≠0$、$γ_2^*=0$：得$x^*=0,γ_1^*=-6<0$，不是K-T点
3. $γ_1^*=0$、$γ_2^*≠0$：得$x^*=5,γ_1^*=-4<0$，不是K-T点
4. $γ_1^*=0$、$γ_2^*=0$：得$x^*=3$，是K-T点

综上$x^*=3$就是其全局极小点。

制约函数法

外点法（惩罚函数）

构造函数$ψ(t) = \begin{cases} 0 & t>0 \\ ∞ & t<0 \end{cases}$，显然有$ψ[g_j(x)] = \begin{cases} 0 & x∈R \\ ∞ & x∉R \end{cases}$

再构造函数

$φ(x) = f(x) + \sum\limits_{j=1}^{l} ψ[g_j(x)]$

这样一来，就把有约束问题的求解化成了求解无约束问题

$\min \ φ(x)$

上述$ψ(t)$在$t=0$处不连续，没有导数。

故重新构造$ψ(t) = \begin{cases} 0 & t≥0 \\ t^2 & t<0 \end{cases}$，则有$\sum\limits_{j=1}^{l} ψ[g_j(x)] \begin{cases} =0 & x∈R \\ ∈(0, ∞) & x∉R \end{cases}$

取$M>0$（$M$充分大），重新构造$φ(x)$为$P(x,M) = f(x) + M\sum\limits_{j=1}^{l} ψ[g_j(x)]$，即

$P(x,M) = f(x) + M\sum\limits_{j=1}^{l} [ \min (0,g_j(x)) ]^2$

$\min P(x, M)$的解$x(M)$即为原问题的极小解或近似极小解。函数$P(x, M)$称为惩罚函数，$M\sum\limits_{j=1}^{l} ψ[g_j(x)]$称为惩罚项，$M$称为惩罚因子。

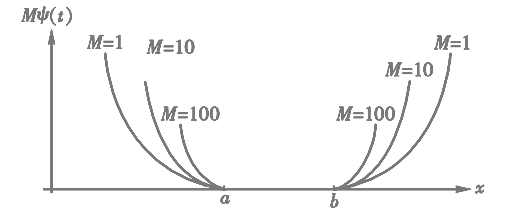
随着$M$得增加惩罚函数中的惩罚项所起的作用随之增大。

例

$\begin{cases} \min f(x) = x_1 + x_2 \\ g_1(x) = -x_1^2 + x_2 ≥ 0 \\ g_2(x) = x_1 ≥ 0 \end{cases}$

解

从$\begin{cases} -x_1^2 + x_2 < 0 \\ x_1 < 0 \end{cases}$构造，从外侧趋近，即外点法。

构造$P(x,M) = (x_1 + x_2) + M\left\{ [ \min (0, (-x_1^2 + x_2)) ]^2 + [ \min (0, x_1) ]^2 \right\}$

• $\dfrac{∂P}{∂x_1} = 1 + 2M\left\{ (-x_1^2 + x_2)(-2x_1) + x_1 \right\}$
• $\dfrac{∂P}{∂x_2} = 1 + 2M\left\{ (-x_1^2 + x_2) \right\}$

令$\begin{cases} \dfrac{∂P}{∂x_1} = 0 \\ \\ \dfrac{∂P}{∂x_2} = 0 \end{cases}$，得$\begin{cases} x_1 = \dfrac{-1}{2(1+M)} \\ \\ x_2 = \dfrac{1}{4(1+M)^2} - \dfrac{1}{2M} \end{cases}$，即有$\min P(x, M)$的解

$x(M) = \left[\begin{matrix} \dfrac{-1}{2(1+M)} \\ \dfrac{1}{4(1+M)^2} - \dfrac{1}{2M} \end{matrix}\right]$

$M = \begin{cases} 1 ⇒ x=\left[ {-\dfrac{1}{4}, -\dfrac{7}{16}} \right]^T \\ 2 ⇒ x=\left[ {-\dfrac{1}{6}, -\dfrac{2}{9}} \right]^T \\ 3 ⇒ x=\left[ {-\dfrac{1}{8}, -\dfrac{29}{192}} \right]^T \\ 4 ⇒ x=\left[ {-\dfrac{1}{10}, -\dfrac{23}{200}} \right]^T \end{cases}$

综上，当$M→∞$时，$x(M)→[0, 0]^T$，即$x_{min}=[0, 0]^T$。

内点法（障碍函数）

如果要求每次迭代得到的近似解都在可行域内，以便观察目标函数值的变化情况；或者，如果$f(x)$在可行域外的性质比较复杂，甚至没有定义，这时就无法使用外点法。

当越接近边界时，惩罚越大。

$\begin{matrix} \bar{P}(x, r_k) = f(x) + r_k\sum\limits_{j=1}^{l} \dfrac{1}{g_j(x)} & r_k>0 \end{matrix}$

或

$\begin{matrix} \bar{P}(x, r_k) = f(x) - r_k\sum\limits_{j=1}^{l} \log[g_j(x)] & r_k>0 \end{matrix}$

$r_k\sum\limits_{j=1}^{l} \dfrac{1}{g_j(x)}$ 或 $-r_k\sum\limits_{j=1}^{l} \log[g_j(x)]$称为障碍项。

例

$\begin{cases} \min f(x) = \dfrac{1}{3}(x_1+1)^3 + x_2 \\ g_1(x) = x_1 - 1 ≥ 0 \\ g_2(x) = x_2 ≥ 0 \end{cases}$

构造障碍函数$\bar{P}(x, r) = \dfrac{1}{3}(x_1+1)^3 + x_2 + \dfrac{r}{x_1-1} + \dfrac{r}{x_2}$

• $\dfrac{∂\bar{P}}{∂x_1} = (x_1+1)^2 - \dfrac{r}{ (x_1-1)^2 }$
• $\dfrac{∂\bar{P}}{∂x_2} = 1 - \dfrac{r}{ {x_2}^2 }$

令$\begin{cases} \dfrac{∂P}{∂x_1} = 0 \\ \\ \dfrac{∂P}{∂x_2} = 0 \end{cases}$，得$\begin{cases} x_1(r) = \sqrt{1 + \sqrt{r}} \\ \\ x_2(r) = \sqrt{r} \end{cases}$

综上$x_{min} = \lim\limits_{r→0} \left[\begin{matrix} \sqrt{1 + \sqrt{r}} \\ \sqrt{r} \end{matrix}\right] = [1, 0]^T$