线性规划（Linear Programming）：导论

• 线性规划（Linear Programming）：导论
  • 基本思想
  • 不等式转等式
    • 剩余变量
    • 松弛变量
  • 表示形式
    • 一般形式
    • 标准型
    • Example
      • 例
  • 解的概念
    • 基
    • 解的状况
  • 几何意义
    • 凸集

基本思想

有限得资源获得最大收益。

不等式转等式

剩余变量

假设存在不等式

$x_1 + x_2 ≤ b$

现新增一个变量$x_3$，将不等式转化为等式

$x_1 + x_2 + x_3 = b$

$x_3$即称为剩余变量。

松弛变量

同理，若有

$x_1 + x_2 ≥ b$

则转换为

$x_1 + x_2 - x_3 = b$

此时$x_3$称为松弛变量。

表示形式

一般形式

$\{\max | \min \} \,\,\, z = c_1x_1 + c_2x_2 + \cdots + c_nx_n$
$\begin{cases} a_{11}x_1 + \cdots + a_{1n}x_n \,\,\, \{ ≤ | = | ≥ \} \,\,\, b_1 \\ \cdots \\ a_{m1}x_1 + \cdots + a_{mn}x_n \,\,\, \{ ≤ | = | ≥ \} \,\,\, b_m \\ x_1, x_2, \cdots, x_n ≥ 0 \end{cases}$

标准型

$\max \,\,\, z = c^Tx$
$\begin{cases} Ax = b \\ x_j ≥ 0 \end{cases}$

• $c$：价值向量
• $a$：技术矩阵
• $b$：资源向量
• $x$：决策向量

每个约束条件都不可缺省，所以矩阵$A_{m×n}$应该是行满秩矩阵，即$r(A)=m ≤ n$。

Example

例

有一般形

$\max \,\,\, z = 2x_1 + 3x_2$
$\begin{cases} x_1 + 2x_2 ≤ 80 \\ 4x_1 ≤ 160 \\ 4x_2 ≤ 120 \\ x_1, x_2 ≥ 0 \end{cases}$

转化为标准型得

$\max \,\,\, z = 2x_1 + 3x_2 + 0x_3 + 0x_4 + 0x_5$
$\begin{cases} x_1 + 2x_2 + x_3 = 80 \\ 4x_1 + x_4 = 160 \\ 4x_2 + x_5 = 120 \\ x_1, x_2, x_3, x_4, x_5 ≥ 0 \end{cases}$

解的概念

• 可行解：满足约束条件（$Ax = b$、$x_j ≥ 0$）的解。
• 可行域：所有可行解的集合。
• 最优解：使目标函数达到最大值的可行解。

基

$B_{m×m}$是约束方程$A_{m×n}$的非奇异子矩阵（即$r(B)=m$、$|B|≠0$），称$B$是线性规划的一个基，最多有$C_n^m$个基。

基解

$Ax=b$
$\,\,\, ⇒ \,\,\, \left[\begin{array}{c} B & N \end{array}\right] \left[\begin{array}{c} x_B \\ x_N \end{array}\right] =b$
$\,\,\, ⇒ \,\,\, Bx_B + Nx_N = b$
$\,\,\, ⇒ \,\,\, x_B = B^{-1}b - B^{-1}Nx_N$

$x_B$即为基解。

基可行解

满足非负约束条件（$x_j ≥ 0$）的基解，称为基可行解，此时的基称为可行基。

解的状况

几何意义

线性规划问题的可行域是一个凸集。

凸集

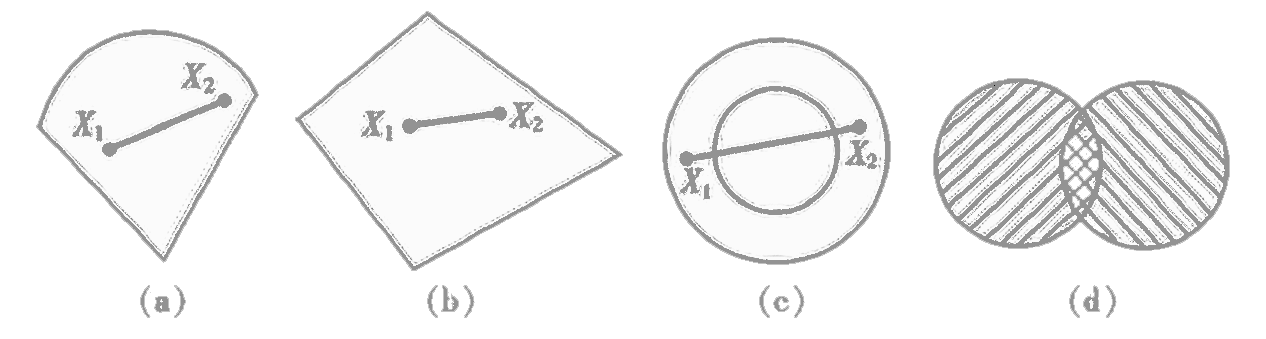
从直观上将，凸集没有凹入部分，其内部没有空洞。

(a)、(b)是凸集，(c)不是凸集，任何两个凸集的交集是凸集(d)。