线性规划（Linear Programming）：对偶理论

• 线性规划（Linear Programming）：对偶理论
  • 对偶问题关系
    • 标准型
    • 非标准型
      • 例
  • 对偶性质
    • 一般性质
    • 互补松弛定理
      • 例
  • 对偶单纯形法
    • 解法
      • 例

对偶问题关系

标准型

原问题

$\max \,\,\, z = c^Tx$
$\begin{cases} Ax ≤ b \\ x ≥ 0 \end{cases}$

对偶问题

$\min \,\,\, ω = b^Ty$
$\begin{cases} A^Ty ≥ c \\ y ≥ 0 \end{cases}$

非标准型

$\begin{array}{r c l} \hline 原问题 & → & 对偶问题 \\ \hline \\ x ≥ 0 & → & A^Ty ≥ c \\ x ≤ 0 & → & A^Ty ≤ c \\ x± & → & A^Ty = c \\ \hline \\ Ax ≤ b & → & y≥0 \\ Ax ≥ b & → & y≤0 \\ Ax = b & → & y± \\ \hline \end{array}$

例

已知
$\max \,\,\, z = 4x_1 + 5x_2$
$\begin{cases} 3x_1 + 2x_2 ≤ 20 \\ 4x_1 - 3x_2 ≥ 10 \\ x_1 + x_2 = 5 \\ x_1≥0, x_2± \end{cases}$

求其非标准型的对偶变换

• $x= \left[\begin{array}{c} x_1 & x_2 \end{array}\right]^T$
• $y= \left[\begin{array}{c} y_1 & y_2 & y_3 \end{array}\right]^T$
• $c= \left[\begin{array}{c} 4 & 5 \end{array}\right]^T$
• $b= \left[\begin{array}{c} 20 & 10 & 5 \end{array}\right]^T$
• $A= \left[\begin{array}{c} 3 & 2 \\ 4 & -3 \\ 1 & 1 \end{array}\right]$

解

• Step1：$\min \,\,\, ω = 20y_1 + 10y_2 + 5y_3$
• Step2：$A^Ty$与$c$的关系
  • $x_1≥0 \,\,⇒\,\, ≥ 4$
  • $x_2± \,\,⇒\,\, = 5$
• Step3：$y$的约束
  • $≤ 20 \,\,⇒\,\, y_1≥0$
  • $≥ 10 \,\,⇒\,\, y_2≤0$
  • $= 5 \,\,⇒\,\, y_3±$

综上

$\min \,\,\, ω = 20y_1 + 10y_2 + 5y_3$
$\begin{cases} 3y_1 + 4y_2 + y_3 ≥ 4 \\ 2y_1 - 3y_2 + y_3 = 5 \\ y_1≥0, y_2≤0, y_3± \end{cases}$

对偶性质

一般性质

弱对偶性

若$\bar{x}$、$\bar{y}$分别是原问题和对偶问题的可行解，则存在$c^T\bar{x}≤b^T\bar{y}$。

无界性

• 如果原（对偶）问题为无界解，则其对偶（原）问题无可行解。
• 当原（对偶）问题为无可行解，其对偶（原）问题具有无界解或无可行解。

强对偶性

若$\hat{x}$、$\hat{y}$分别是原问题和对偶问题的可行解，当$c^T\hat{x}=b^T\hat{y}$时$\hat{x}$、$\hat{y}$分别是对应问题的最优解。

对偶定理

若原问题和对偶问题两者皆可行，则两者均有最优解，且此时目标函数值相等。

对偶问题的解必然是下列三种情况之一：

• 原问题和对偶问题都有最优解。
• 一个问题具有无界解，另一个问题无可行解。
• 原问题和对偶问题都无可行解。

互补松弛定理

设$\hat{x}$、$\hat{y}$分别是原问题和对偶问题的可行解，$x_s$为原问题的松弛变量的值，$y_s$为对偶问题剩余变量的值。

$\begin{cases} A\hat{x} + x_s = b & \hat{x}, x_s ≥ 0 \\ A^T\hat{y} - y_s = c & \hat{y}, y_s ≥ 0 \end{cases}$

• $\begin{cases} A\hat{x} + x_s = b \\ \hat{y}^TA - y_s^T = c^T \end{cases}$
• $\begin{cases} \hat{y}^TA\hat{x} + \hat{y}^Tx_s = \hat{y}^Tb \\ \hat{y}^TA\hat{x} - y_s^T\hat{x} = c^T\hat{x} \end{cases}$
• $\hat{y}^Tx_s + y_s^T\hat{x} = \hat{y}^Tb - c^T\hat{x}$
• 若$\hat{y}^Tx_s + y_s^T\hat{x} = 0$，则$\hat{y}^Tb - c^T\hat{x} = 0$，即$(\hat{y},b) = (c,\hat{x})$。

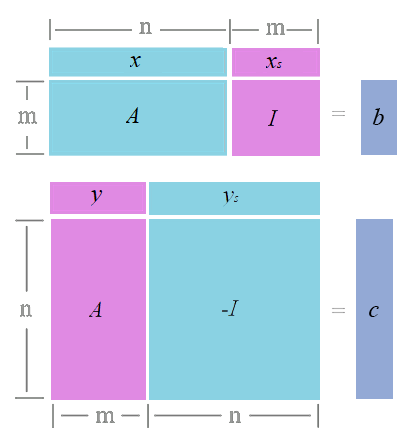
$x^*$、$y^*$分别是原问题和对偶问题最优解的充要条件是$(y^*,x_s) + (y_s,x^*) = 0$，或

$(y^*,x_s) = 0, (y_s,x^*) = 0$

即，原问题的解及其对偶模型的松弛变量（剩余变量）（明显数量是相同的），必有一个为0。

例

原问题

$\min \,\,\, ω = 2x_1 + 3x_2 + 5x_3 + 2x_4 + 3x_5$
$\begin{cases} x_1 + x_2 + 2x_3 + x_4 + 3x_5 ≥ 4 \\ 2x_1 - x_2 + 3x_3 + x_4 + x_5 ≥ 3 \\ x_j≥0, j=1,2,3,4,5 \end{cases}$

已知其对偶问题的最优解为

$\begin{cases} y_1^* = \frac{4}{5} \\ y_2^* = \frac{3}{5} \\ z = 5 \end{cases}$

试找出原问题最优解。

解

对偶问题为

$\max \,\,\, z = 4y_1 + 3y_2$
$\begin{cases} y_1 + 2y_2 ≤ 2 \\ y_1 - y_2 ≤ 3 \\ 2y_1 + 3y_2 ≤ 5 \\ y_1 + y_2 ≤ 2 \\ 3y_1 + y_2 ≤ 3 \\ y_1, y_2 ≥ 0 \end{cases}$

带入$y_1^*$、$y_2^*$。

$\begin{cases} ①: (y_1 + 2y_2 = 2) + y_{s1}= 2 \\ ②: (y_1 - y_2 = \frac{1}{5}) + y_{s2} = 3 \\ ③: (2y_1 + 3y_2 = \frac{17}{5}) + y_{s3} = 5 \\ ④: (y_1 + y_2 = \frac{7}{5}) + y_{s4} = 2 \\ ⑤: (3y_1 + y_2 = 3) + y_{s5} = 3 \end{cases}$

• $y_{s1} = y_{s5} = 0$
• $y_{s2}≠0, y_{s3}≠0, y_{s4}≠0$

由互补松弛性（$y_{si} ⋅ x_{i}^* = 0$）得

$x_2^* = x_3^* = x_4^* = 0$

又因为$y_1, y_2 ≥ 0$，由互补松弛性（$y_i^* ⋅ x_{si} = 0$）得

$x_{s1} = x_{s2} = 0$

综上得

$\begin{cases} x_1^* + 0 + 0 + 0 + 3x_5^* + 0 = 4 \\ 2x_1^* - 0 + 0 + 0 + x_5^* + 0 = 3 \\ x_j≥0, j=1,2,3,4,5 \end{cases}$

计算得

$x_1^* = 1, x_5^* =1, ω^* = 5$

对偶单纯形法

解法

• Step1：选
  • 选出$b$最小的行$i$作为离基。
  • 在行$i$中选出$\left|\dfrac{σ_j}{a_{ij}}\right|$（$a_{ij}<0$，若均为非负则无可行解）最小的列$j$为进基。
  • $i$、$j$的交叉点为主元$a_{ij}$。
• Step2：消
  • $\dfrac{row(i)}{a_{ij}}$
  • $\underset{k\ in\ row,k≠i}{for} [row(k) - a_{kj}row(i)]$
• Step3：换
  • 行$i$，$x_B$更换为进基变量
  • 行$i$，$C_B$更换为进基$c_j$
• Step4：重新计算$σ$。
• Step5：重复上述操作，直到每行都满足$b≥0$。

例

$\min \,\,\, ω = x_1 + 4x_2 + 3x_4$
$\begin{cases} x_1 + 2x_2 - x_3 + x_4 ≥ 3 \\ -2x_1 - x_2 + 4x_3 + x_4 ≥ 2 \\ x_j≥0, j=1,2,3,4 \end{cases}$

引入松弛变量，转化为标准型

注意此处不等式先转换为$≤$再添加松弛变量。

$\min \,\,\, ω = x_1 + 4x_2 + 3x_4$
$\begin{cases} -x_1 - 2x_2 + x_3 - x_4 + x_5 = -3 \\ 2x_1 + x_2 - 4x_3 - x_4 + x_6 = -2 \\ x_j≥0, j=1,2,3,4,5,6 \end{cases}$

解

	$c_j$	1	4	0	3	0	0
$C_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$b$
0	$x_5$	-1	-2	1	-1	1	0	-3
0	$x_6$	2	1	-4	-1	0	1	-2
	$σ_j$	1	4	0	3	0	0
$C_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$b$
1	$x_1$	1	2	-1	1	-1	0	3
0	$x_6$	0	-3	-2	-3	2	1	-8
	$σ_j$	0	2	1	2	1	0
$C_B$	$X_B$	$x_1$	$x_2$	$x_3$	$x_4$	$x_5$	$x_6$	$b$
1	$x_1$	1	$\frac{7}{2}$	0	$\frac{5}{2}$	-2	$-\frac{1}{2}$	7
0	$x_3$	0	$\frac{3}{2}$	1	$\frac{3}{2}$	-1	$-\frac{1}{2}$	4
	$σ_j$	0	$\frac{1}{2}$	0	$\frac{1}{2}$	2	$\frac{1}{2}$

最优解时$x_1=7$、$x_3=4$

$ω = x_1 + 4x_2 + 3x_4 = 7$