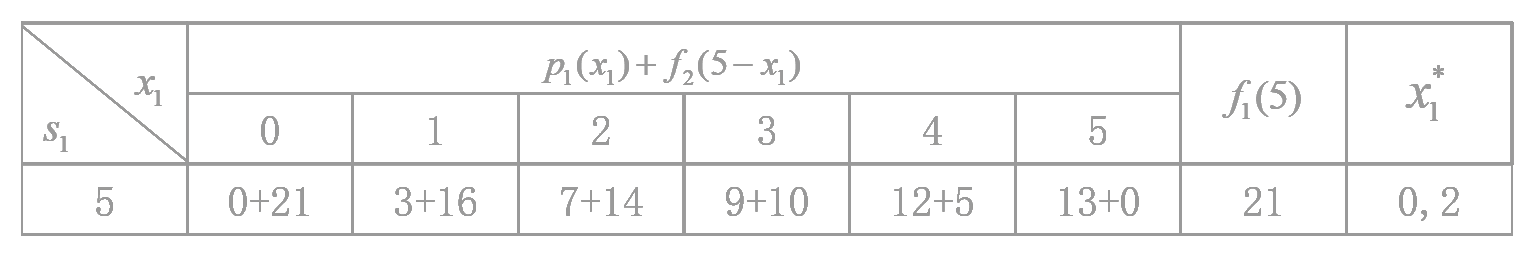动态规划

动态规划

基本概念

动态规划是解决多阶段决策过程最优化的一种数学方法。

马尔科夫性

如果某阶段状态给定后，则在这阶段以后过程的发展不受这阶段以前各段状态的影响。换句话说，过程的过去历史只能通过当前的状态去影响它未来的发展，当前的状态是以往历史的一个总结。这个性质称为无后效性（即马尔科夫性）。

最优性原理

无论过去的状态和决策如何，对前面的决策所形成的状态而言，余下的诸决策必须构成最优策略。即，最优策略的子策略总是最优的。可以利用该原理，通过局部最优来逆推全局最优。

动态规划和静态规划

线性规划和非线性规划研究的问题通常与时间无关，故又称为静态规划。
动态规划、静态规划都属于数学规划范围，都是在若干约束条件下的函数极值问题，都利用迭代法去逐步求解。
一些静态规划只要适当引入阶段变量、状态、决策等就可以转化为动态规划问题。
动态规划研究的问题与时间有关，研究具有多阶段决策过程的一类问题，将问题的整体按时间或空间的特征分成若干个前后衔接的时空阶段，把多阶段决策问题表示为前后有关联的一系列单阶段决策问题，然后逐个加以解决，从而求出整个问题的最优决策序列。

规划类型	内容	与时间关系	问题类型	解决方案
静态规划	线性规划、非线性规划	无关		一定条件下可转换为动态规划问题
动态规划	动态规划	有关	多阶段决策

解决动态规划的方法

解法	适用情况
逆序解法	已给定初始状态
顺序解法	已给定终止状态

例

$\max z = x_1 ⋅ {x_2}^2 ⋅ x_3$
$\begin{cases} x_1 + x_2 + x_3 = c & c>0 \\ x_i ≥ 0, & i = 1,2,3 \end{cases}$

使用逆推法解答上述问题。

解

设第 $k$ 阶段初始状态为 $s_k$ ，有最优值函数 $f_k(s_k)$ 。

令 $\begin{cases} s_3 = x_3 & ⇒\ \ \ 0 ≤ x_3 = s_3 \\ s_2 = x_2 + s_3 & ⇒\ \ \ 0 ≤ x_2 ≤ s_2 \\ s_1 = x_1 + s_2 = c & ⇒\ \ \ 0 ≤ x_1 ≤ s_1 = c \end{cases}$

根据逆推法（最优解从后向前传递）有

$\begin{array}{l} f_3(s_3) = \max\limits_{s_3 = x_3} (x_3) \\ f_2(s_2) = \max\limits_{0 ≤ x_2 ≤ s_2} [{x_2}^2f_3(s_3)] \\ f_1(s_1) = \max\limits_{0 ≤ x_1 ≤ s_1} [{x_1}f_2(s_2)] \end{array}$

明显 $f_3(s_3)$ 有最优值 $s_3$ ，递推有

$f_2(s_2) = \max\limits_{0 ≤ x_2 ≤ s_2} {x_2}^2(s_2-x_2) \xrightarrow{记作} \max\limits_{0 ≤ x_2 ≤ s_2} h_2(s_2, x_2)$

$\dfrac{∂h_2}{∂x_2} = 2x_2s_2 - 3{x_2}^2 = 0 \ \ \ ⇒ \ \ \ x_2 = \dfrac{2}{3}s_2$
$\dfrac{∂h_2}{∂{x_2}^2} = 2s_2 - 6x_2$ ， $\dfrac{∂h_2}{∂{x_2}^2}\Big|_{x_2 = \frac{2}{3}s_2} = -2s_2 < 0$

故 $f_2(s_2)\Big|_{x_2 = \frac{2}{3}s_2} = \dfrac{4}{27} {s_2}^3$ ，继续递推有

$f_1(s_1) = \max\limits_{0 ≤ x_1 ≤ s_1} x_1 \dfrac{4}{27} (s_1 - x_1)^3 \xrightarrow{记作} \max\limits_{0 ≤ x_1 ≤ s_1} h_1(s_1, x_1)$

$\dfrac{∂h_1}{∂x_1} = 0 \ \ \ ⇒ \ \ \ x_1 = \dfrac{1}{4}s_1$

综上

$\begin{cases} x_1 = \dfrac{1}{4}c \\ x_2 = \dfrac{2}{3}(c - x_1) = \dfrac{1}{2}c \\ x_3 = s_3 = s_2 - x_2 = \dfrac{1}{4}c \end{cases}$

$\max z = f_1(s_1) = \dfrac{1}{64}{s_1}^4 = \dfrac{1}{64}c^4$

最优路径问题

求解方法

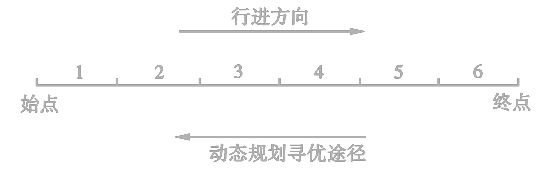
如果由起点 $A$ 经过 $P$ 点和点 $H$ 而到达终点G是一条最短路线，则由点 $P$ 出发经过 $H$ 点到达终点 $G$ 的这条子路线，对于从点 $P$ 出发到达终点的所有可能选择的不同路线来说，必定也是最短路线。

寻找最短路线的方法，就是从最后一段开始，用由后向前逐步递推的方法，求出各点到G点的最短路线，最后求得由A点到G点的最短路线。

资源分配问题

将数量一定的一种或若干种资源，恰当地分配给若干个使用者，且使目标函数为最优。

在应用动态规划方法处理这类静态规划问题时，通常以把资源分配给一个或几个使用者的过程作为一个阶段，把问题中的变量xi为决策变量，将累计的量或随递推过程变化的量选为状态变量。

例

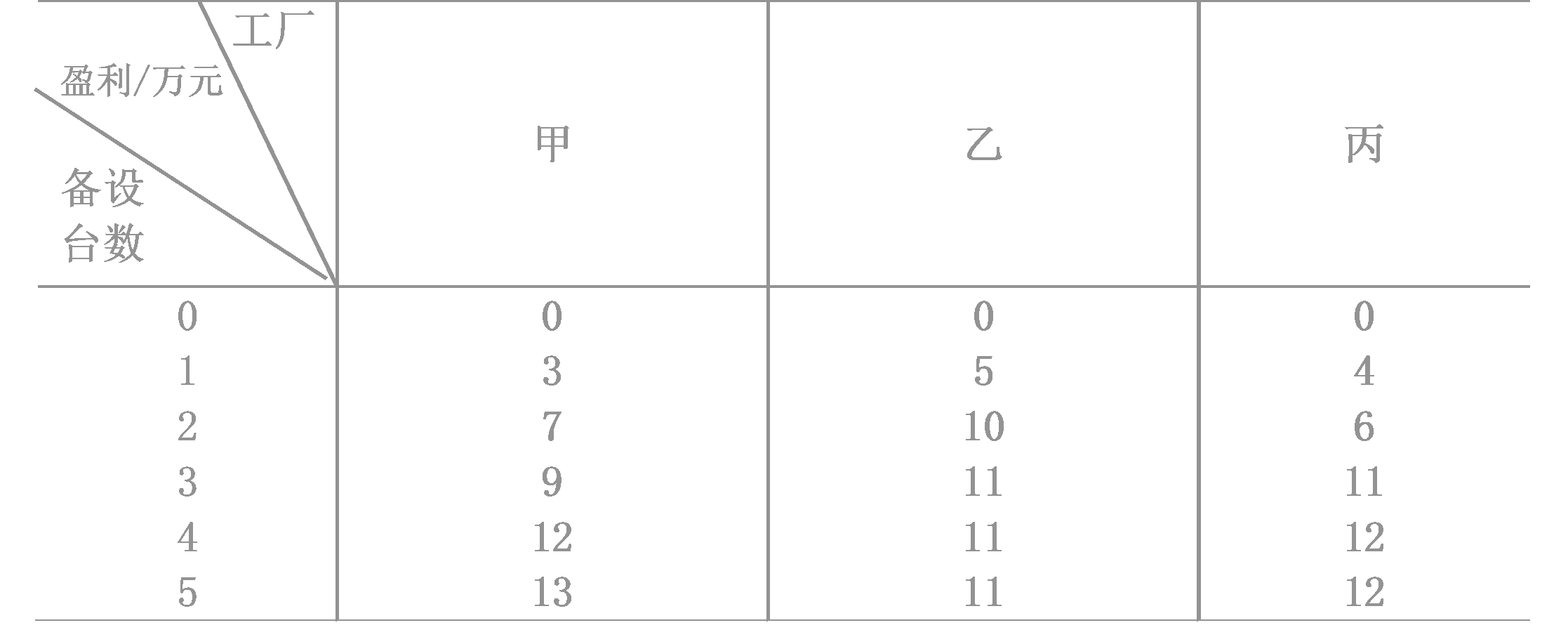
这五台设备如何分配给甲乙丙各工厂，才能使盈利最大。

解

将分配过程分为三个阶段

给甲厂分配 $x_1$ 台
给乙厂分配 $x_2$ 台
给丙厂分配 $x_3$ 台

	甲	乙	丙
$s_1$	√	√	√	$s_1 = \sum_{i=1}^{n} x_i = 5$
$s_2$	×	√	√	$s_2 = s_1 - x_1 = x_2 + x_3$
$s_3$	×	×	√	$s_3 = s_2 - x_2 = x_3$
$s_4$	×	×	×	$s_4 = s_3 - x_3 = 0$

$\begin{cases} f_k(s_k) = \max\limits_{0≤x_k≤s_k} [P_x(x_k) + f_{k+1}(s_k - x_k)] & k=3,2,1 \\ f_4(s_4) = 0 \end{cases}$

$x_k$ ：分配给第 $k$ 个工厂的设备台数
$s_k$ ：分配给第 $k$ 个至第 $n$ 个工厂一共的设备台数
$P_k(x_k)$ ： $x_k$ 台设备分配到第 $k$ 个工厂所得的盈利值
$f_k(s_k)$ ： $s_k$ 台设备分配到第 $k$ 个至第 $n$ 个工厂一共所得的盈利值

使用逆推法

$f_3(s_3) = \max\limits_{x_3} [P_3(x_3) + f_4(s_4)] = \max\limits_{x_3} P_3(x_3)$

因为此时只有一个工厂，有多少台设备就全部分配给工厂丙，故它的盈利值就是该段的最大盈利值。

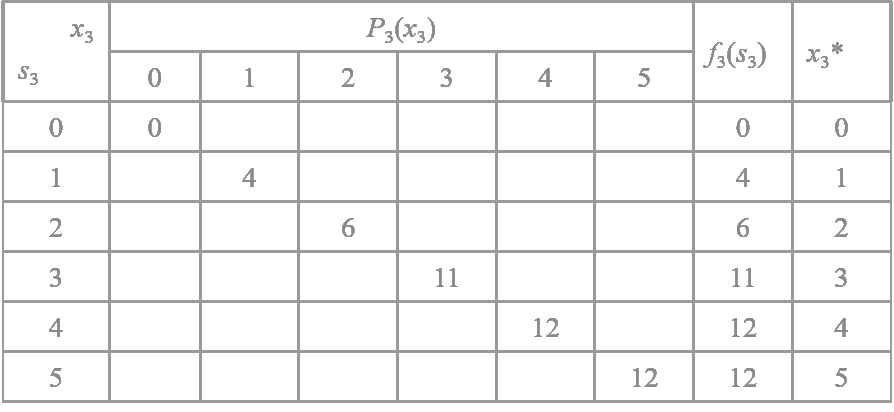
$f_2(s_2) = \max\limits_{x_2} [P_2(x_2) + f_3(s_2 - x_2)]$

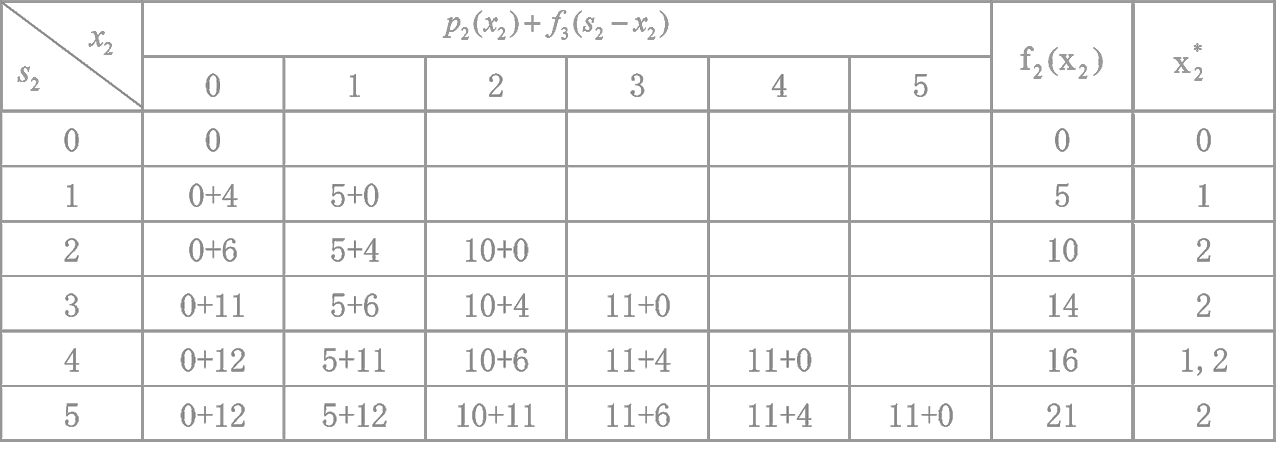
$f_1(5) = \max\limits_{x_1} [P_1(x_1) + f_2(5 - x_1)]$

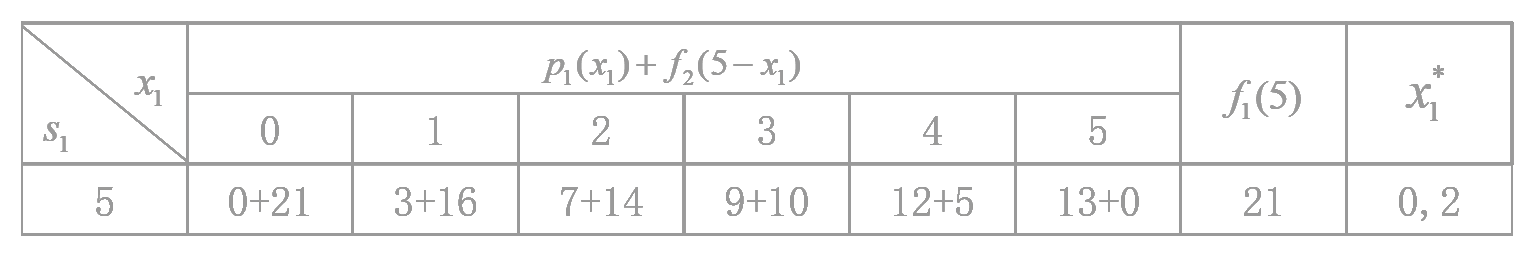
综上可得

$\begin{cases} x_1 = 2 \\ x_2 = 2 \\ x_3 = 1 \\ \max f_1(5) = 21 \end{cases}$