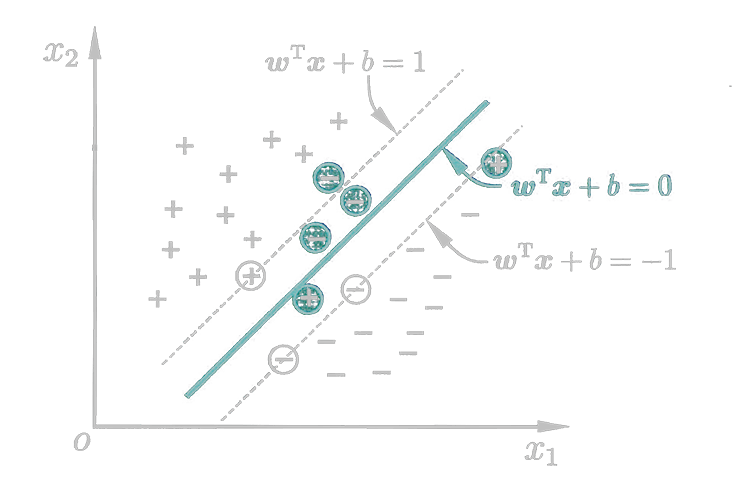
点到超平面的距离
r=∥w∥∣wT+b∣
若超平面(w,b)能正确分类,对于(xi,yi)∈D有
{wTxi+b≥1wTxi+b≤−1yi=+1yi=−1
距离超平面最近的几个训练样本上的点使上式成立,被称为支持向量(SV,Support Vector)。训练完成后,大部分样本都不需要保留,最终模型仅与支持向量有关。
注:此处我们人为的规定了wTxi+b=±1xi∈SV。
两个异类支持向量到超平面的距离和称作间隔(Margin)
γ=∥w∥2
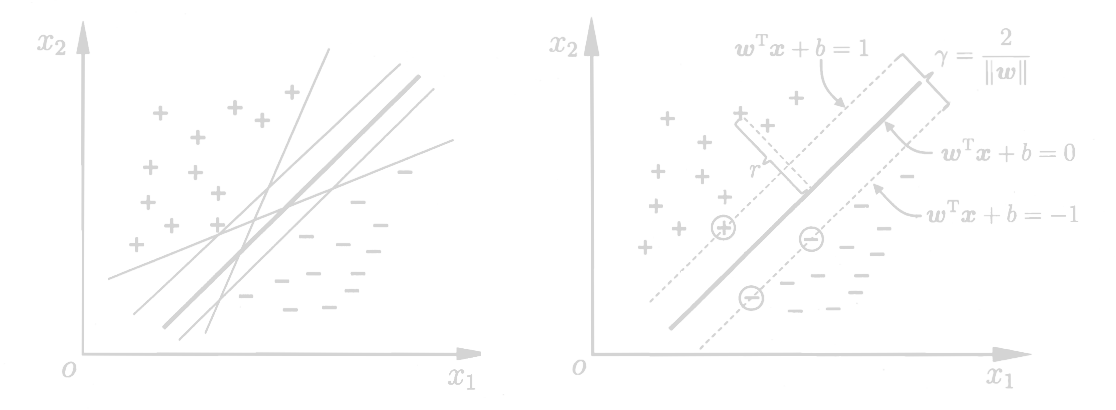
寻找最大间隔γ等效于寻找最小的∥w∥2=wTw
⎩⎪⎪⎪⎨⎪⎪⎪⎧w,bmin21wTwyi(wTxi+b)≥1
上式即为支持向量机(Support Vector Machine)的基本型。这是一个标准的二次规划问题。
拉格朗日(Lagrange)乘数法:该方法通过增加变量,将一个约束问题转换为一个无约束问题
{f(x,y)φ(x,y)=0 ⇒ L(x,y,λ)=f(x,y)+λφ(x,y)
使用原问题引入非线性变换时,会使特征维度很大,计算复杂度很高。通过变换,将会产生一个和特征维度无关的新问题。
对原问题使用拉格朗日乘数法去掉约束,有
L(w,b,α)=21wTw+i=1∑mαi[1−yi(wTxi+b)]
- m:样本数
- α=[α1α2⋯αm]T
有弱对偶关系(可理解为:凤尾≥鸡头)
b,wmin[αi≥0maxL(w,b,α)]≥αi≥0max[b,wminL(w,b,α)]
注:实际是满足强对偶关系的,但因证明过于复杂,此处省略。
优化目标
αi≥0max[b,wmin(21wTw+i=1∑mαi[1−yi(wTxi+b)])]
继续求解
⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∂w∂L=0∂b∂L=0 ⇒ ⎩⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧w=i=1∑mαiyixi0=i=1∑mαiyi
将解带回优化目标得对偶问题
⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxji=1∑mαiyi=0αi≥0i=1,⋯,m
该方法可以解出对偶问题中的α。
st=>start: 开始
op1=>operation: 选取一对需更新的α_i、α_j
op2=>operation: 固定其它参数,获得更新后的α_i、α_j
con=>condition: 结果是否已经足够收敛?
output=>inputoutput: 输出α
ed=>end: 结束
st->op1->op2->con
con(no)->op1
con(yes)->output->ed
代入的α得最终模型
f(x)=wTx+b=i=1∑mαiyixiTx+b
⎩⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧αi≥0yif(xi)−1≥0αi[yif(xi)−1]=0
当训练样本不是线性可分的时候,可以将样本从原始空间映射到一个更高维的空间,这样就能找到一个合适的划分超平面。
如果原始空间维数有限(属性有限),就一定存在一个高维特征空间使样本可分。
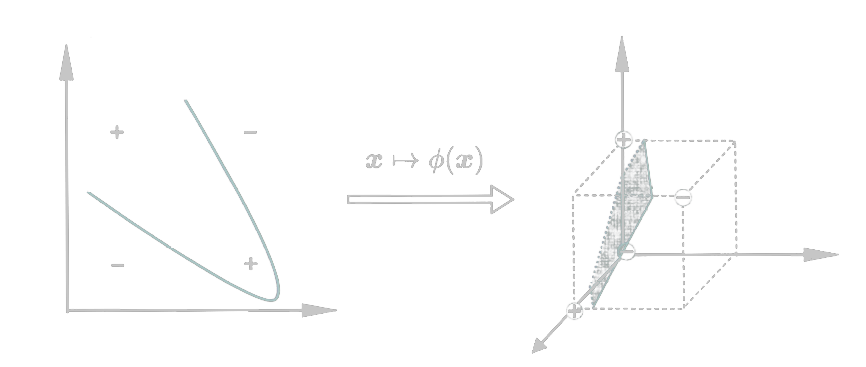
αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjϕ(xiT)ϕ(xj)
允许一些样本出错,即允许某些样本不满足约束条件。