机器学习:神经网络
基本神经网络
M-P神经元
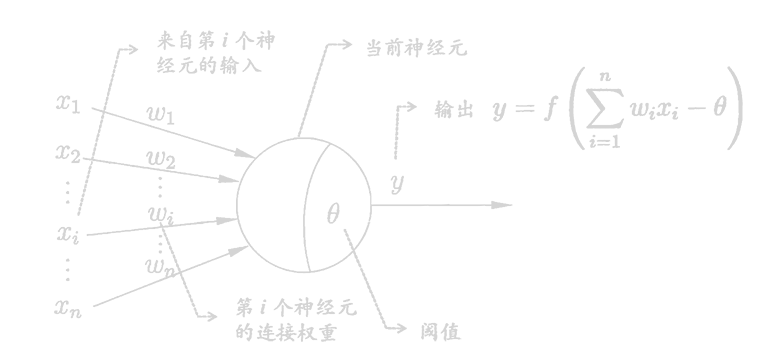
感知机(Perceptron)
由两层神经元组成,输出层是M-P神经元,仅有输出层神经元进行激活函数处理。
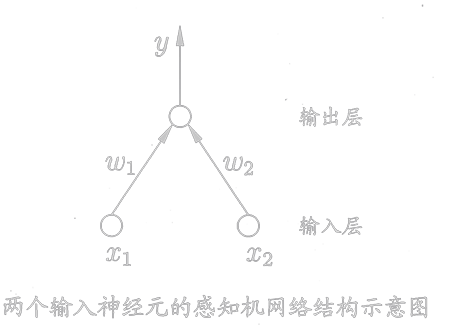
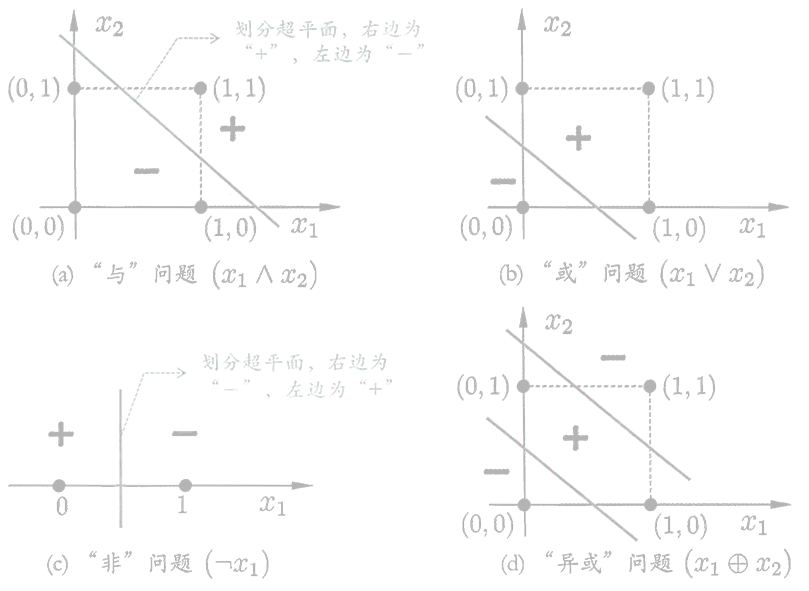
感知机模型仅能解决一个线性可划分问题,所以感知机模型不能解决异或问题。
隐藏层
输入层与输出层之间的一层神经元称为隐藏层(隐含层,Hidden Layer)。隐藏层和输出层都有激活函数处理。
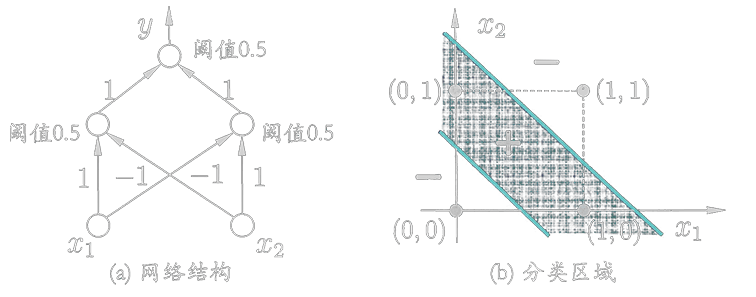
以上多层神经网络可以解决异或问题。
多层感知器(MLP,Multilayer Perceptron)
多层前馈神经网络(Multi-layer Feedforward Neural)
误差逆传播(errorBackPropagation)
BP算法基于梯度下降(Gradient Descent)策略,以目标的负梯度方向对参数进行调整。
- :学习率,,过大时容易发生震荡
- :第轮训练后的均方误差
- :上一层第个神经元与下一层第个神经元的连接权
工作流程
st=>start: 开始
init=>operation: 初始化连接权和阈值
input=>inputoutput: 输入:训练集、学习率
sub1=>operation: 前向传播:计算输出值、误差
sub2=>operation: 反向传播:计算梯度顶,更新连接权和阈值
isend=>condition: 满足训练次数 Or 满足正确率
output=>inputoutput: 输出:连接权和阈值
ed=>end: 结束
st->init->input
input->sub1->isend
isend(no)->sub2->sub1
isend(yes)->output->ed
最小值
在使用梯度下降法进行搜索时,很可能我们得到的是一个局部极小值。
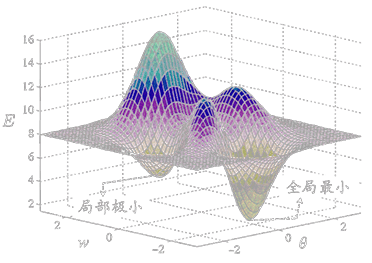
一些常见的跳出局部极小值的方法
- 使用不同参数值初始化多个神经网络,取其中误差最小的解作为最终参数。
- 模拟退火技术:每一步都有一定的概率接受次优解,随着步数增加该概率逐渐下降。
- 随机梯度下降:计算梯度时加入随机因素,即便陷入局部极小点,其计算梯度的梯度值也不为0,使其有可能跳出继续搜索。