机器学习：模型评估

• 机器学习：模型评估
  • 拟合
    • 过拟合（Overfitting）
    • 欠拟合（Underfitting）
  • 模型评估方法
    • 留出法（Hold-out）
    • 交叉验证法（Cross Validation）
    • 自助法（Bootstrapping）
  • 性能度量
    • 均方误差（Mean squared error）
    • 错误率与精度
    • 混淆矩阵
      • 准确率
      • 特异度
      • 精确率（查准率）
      • 召回率（查全率）
      • 平衡点（BEP，Break-Even Point）
      • $F_1$
      • $F_β$
      • ROC
  • 代价
    • 代价敏感（Cost-Sensitive）错误率
    • 代价曲线（Cost Curve）
  • 比较检验
  • 偏差

拟合

过拟合（Overfitting）

略

欠拟合（Underfitting）

略

模型评估方法

留出法（Hold-out）

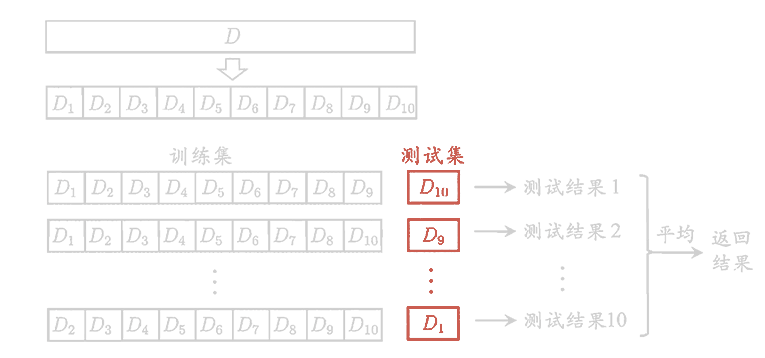
直接将数据集划分为两个互斥地集合，其中一个集合作为训练集，另一个作为测试集。在使用时，一般要采用若干次随机划分，重复进行实验，评估后取平均值作为结果。

交叉验证法（Cross Validation）

自助法（Bootstrapping）

假定包含$m$个样本的数据集$D$，每次从$D$中随机挑选一个样本，将其拷贝入$D'$，重复$m$次，就得到了包含$m$个样本的数据集$D'$。显然，$D$中的一部分样本会在$D'$中多次出现，一部分样本不会在$D'$中出现。该方法在数据集较小，难以有效划分训练集、测试集时很有用，但会引入估计偏差。

性能度量

均方误差（Mean squared error）

$MSE(f, y) = \dfrac{ \sum\limits_{i=1}^{m} [f(x_i) - y_i]^2 }{m}$

回归任务最常用的性能度量方法。

错误率与精度

错误率

$E = \dfrac{ \sum\limits_{i=1}^{m} Ⅱ[f(x_i)≠y_i] }{m}$

精度

$Acc = \dfrac{ \sum\limits_{i=1}^{m} Ⅱ[f(x_i)=y_i] }{m}$

混淆矩阵

真实情况	预测为正例（Positive）	预测为反例（Negatie）
正例（True）	真正例（TP）	伪反例（FN）
反例（False）	伪正例（FP）	真反例（TN）

• $m = TP + FP + TN + FN$

准确率

$Accuracy = \dfrac{TP+TN}{m} = \dfrac{TP+TN}{TP + FP + TN + FN}$

特异度

$Specificity = \dfrac{TN}{False} = \dfrac{TN}{FP + TN}$

精确率（查准率）

$Precision = \dfrac{TP}{Positive} = \dfrac{TP}{TP + FP}$

召回率（查全率）

$Recall = \dfrac{TP}{True} = \dfrac{TP}{TP + FN}$

平衡点（BEP，Break-Even Point）

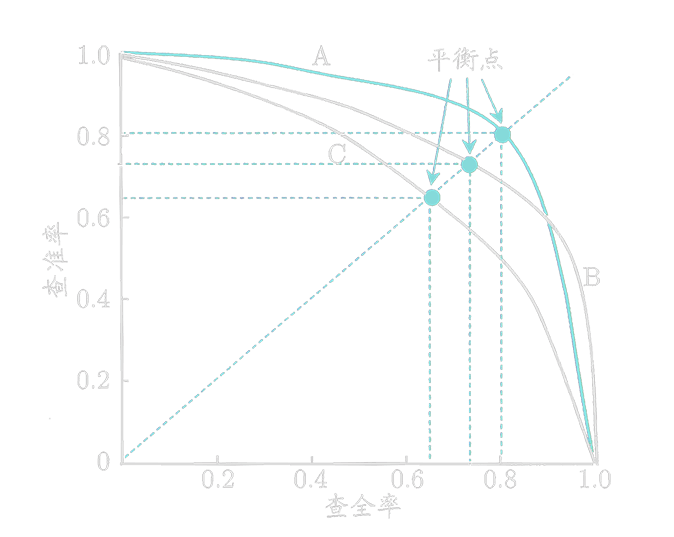
查准率和查全率是一对矛盾的变量，平衡点就是查准率等于查全率时的取值。

$F_1$

$\begin{array}{r} F_1 \\ \\ \\ \\ \\ \\ \\ \end{array} \begin{array}{l} = \dfrac{1}{ \frac{1}{2} ⋅ \frac{1}{Precision} + \frac{1}{2} ⋅ \frac{1}{Recall} } \\ \\ = \dfrac{2 ⋅ Precision⋅Recall}{Precision + Recall} \\ \\ = \dfrac{2TP}{2TP + FN + FP} \end{array}$

$F1$是基于查准率和查全率的调和平均数。

$F_β$

$\begin{array}{r} F_β \\ \\ \\ \\ \\ \end{array} \begin{array}{l} = \dfrac{1}{ \frac{1}{β^2+1} ⋅ \frac{1}{Precision} + \frac{β^2}{β^2+1} ⋅ \frac{1}{Recall} } \\ \\ = \dfrac{ (1+β^2) ⋅ Precision ⋅ Recall }{ β^2 ⋅ Precision + Recall } \end{array}$

$F_β$是基于查准率和查全率的加权调和平均数，当$β=1$时，即为$F_1$。

ROC

ROC（Receiver Operating Characteristic，受试者工作特征）曲线纵轴为“真正例率（TPR，True Positive Rate）”，横轴是“假正例率（FPR，False Positive Rate）”。

• $TPR = \dfrac{TP}{True} = \dfrac{TP}{TP + FN}$
• $FPR = \dfrac{FP}{False} = \dfrac{FP}{FP + TN}$

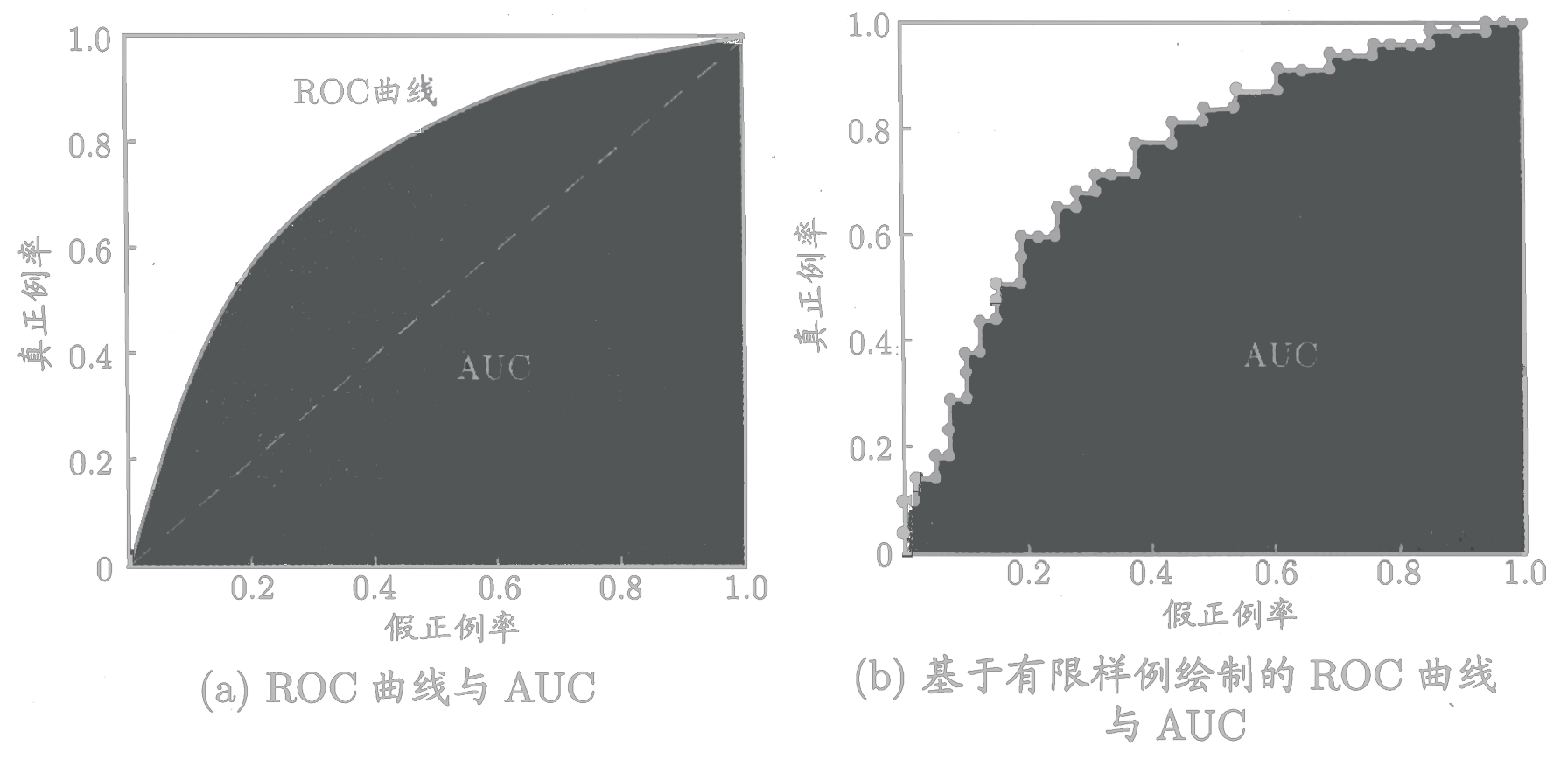
“AUC（Area Under Curve）”为ROC曲线所覆盖的区域面积。AUC越大，分类器分类效果越好。

AUC	效果
$1$	完美分类器
$(0.5,1)$	优于随机猜测
$0.5$	等价于随机猜测
$(0,0.5)$	差于随机猜测

代价

在非均等代价下ROC曲线不能反映出学习器的期望总体代价。

代价敏感（Cost-Sensitive）错误率

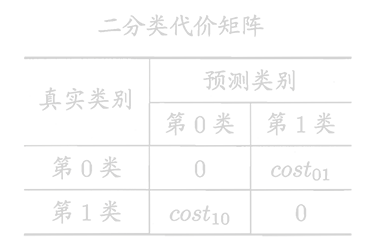
$E = \dfrac{ \sum\limits_{x_i∈D^+} Ⅱ(f(x_i)≠y_i) cost_{01} + \sum\limits_{x_i∈D^-} Ⅱ(f(x_i)≠y_i) cost_{10} }{m}$

• $D^+$：实例集$D$的正例子集。
• $D^-$：实例集$D$的反例子集。

代价曲线（Cost Curve）

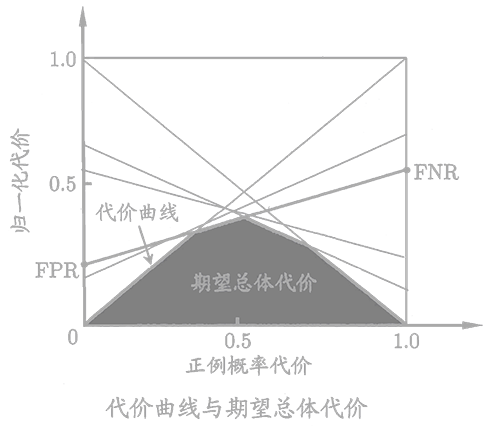
横轴为“正概率代价”，纵轴为“归一化代价”。

$P(+){cost} = \dfrac{ p ⋅ cost_{01} }{ p ⋅ cost_{01} + (1-p) ⋅ cost_{10} }$

• $p$：样例为正例的概率。

$cost_{norm} = \dfrac{ FNR ⋅ p ⋅ cost_{01} + FPR ⋅ (1-p) ⋅ cost_{10} }{ p ⋅ cost_{01} + (1-p) ⋅ cost_{10} }$

• $FNR = \dfrac{FN}{True}$
• $FPR = \dfrac{FP}{False}$

比较检验

我们希望比较的是泛化性能，然而通过实验评估方法我们获得的是测试集上的性能，两者的对比结果未必相同。

比较算法数量	检验名称	说明
2	交叉验证$t$检验
2	$McNemar$检验
*	$Friendman$检验
*	$Nemenyi$后续检验

偏差

偏差

$bias_i = f(x_i) - y_i$

方差

$ε^2 = \dfrac{ \sum\limits_{i=1}^{m} {bias_i}^2 }{m}$

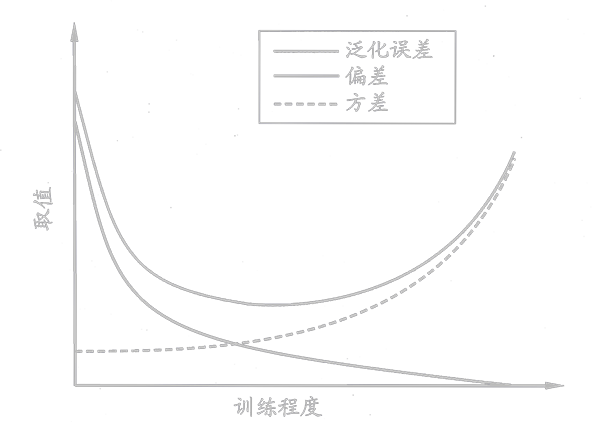
偏差方差窘境（Bias-Variance Dilemma）

一般来说，偏差与方差是有冲突的，假定我们能控制学习算法的训练程度，则在训练不足时，学习器的拟合能力不够强，训练数据的扰动不足以使学习器产生显著变化，此时偏差主导了泛化错误率；随着训练程度的加深，学习器的拟合能力逐渐增强，训练数据发生的扰动渐渐能被学习器学到，方差逐渐主导了泛化错误率。