线性代数的本质:特征值和特征向量
Aλ=λξ, ξ=0
Aλ=λξ, ξ=0
⇒⇒⇒λEξ−Aξ=0(λE−A)ξ=0∣λE−A∣=0
| 特征值 |
特征向量 |
特征多项式 |
特征方程 |
| λ |
ξ |
∣λE−A∣ |
∣λE−A∣=0 |
特征多项式
∣λE−A∣=k=0∑n(−1)ktr[k](A)λn−k=λn−tr[1](A)λn−1+⋯+(−1)n∣A∣
性质
- ∑i=1nλi=tr(A)=i=1∑naii
- ∏i=1nλi=∣A∣
- 不同特征值的特征向量线性无关
几何重数
如果A的属于特征值λs的线性无关特征向量有s个,则称特征值λs的几何重数是s。
代数重数
如果λm是A的特征方程∣λE−A∣=0的m重根,则称特征值λm的代数重数是m。
若A相似于对角阵(记作A∼Λ),则称A可相似对角化,称A为单纯矩阵。
充要条件
- A有n个线性无关的特征向量 ⇔ A可相似对角化
充分条件
- A有n个不同的特征值 ⇒ A可相似对角化
- λi是矩阵A的mi重特征值,且满足mi=n−r(A−λiE) ⇒ A可相似对角化
∣a+bi∣=a2+b2
以矩阵第i行第i个元素的(a,b)为圆心(a为元素实部、b为元素虚部),第i行其它元素的模的和为半径,刻画⚪(实边)到复平面上。则n阶矩阵可画n个圆盘。
定理1
特征值属于所有⚪的并集。
定理2
每个连续的独立的部分,有几个⚪就有几个特征值。
- n个圆盘都不相交 ⇒ A可相似对角化
- 若A为实矩阵,对特征多项式进行分解
- 分解出一个一次项,出来一个实根
- 分解出一个二次项,出现一对虚根,即实矩阵虚根一出出一对
- n个圆盘都不相交且A是实矩阵 ⇒ A的特征值全是实数
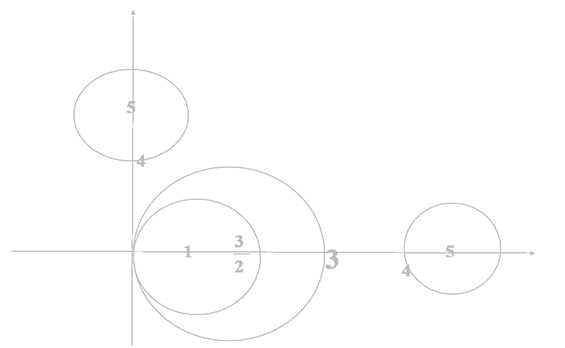
A=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡1−210−1−2123−2i0−21i50002i5i⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
画出矩阵A的圆盘图
解
A4×4=⎣⎢⎢⎢⎡90−121800−21401−40−1⎦⎥⎥⎥⎤
证明A至少有两个实根。
解
A为实矩阵,所以
∣λE−A∣=λ4+a2λ3+a3λ2+a4λ+∣A∣
为实系数多项式。
左侧仅有一个根,且必为实根(因为虚根成对出现)。
右侧有三个根,可能存在如下两种情况
综上,A至少有两个实根。
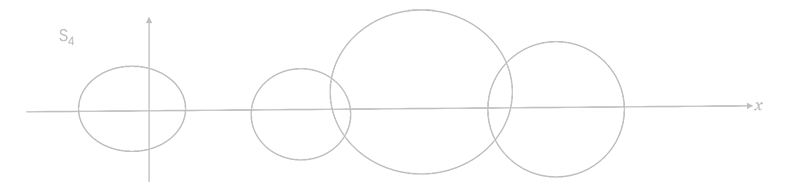
A=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡45161⋮n+31415(61)2⋮(n+31)2(41)2(51)26⋮⋯⋯⋯⋯⋱(n+31)n−1(41)n−1(51)n−1(61)n−1⋮n+3⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤
证明矩阵A所有特征值都为实数,且可逆,可相似对角化。
解
- 等比数列前n项和:Sn=a11−r1−rn
- 1+r+r2+⋯+rn−1=1−r1−rn
- r+r2+⋯+rn−1=1−rr−rn
- S4(n−1)=41+(41)2+(41)3+⋯+(41)n−1=1−4141−(41)n=31(1−4n−11)<31<21
- S5(n−1)=51+(51)2+(51)3+⋯+(51)n−1=1−5151−(51)n=41(1−5n−11)<41<21
- Si(n−1)=i−11(1−in−11)<i−11<21, i≥4
故可以画出圆盘图如下图所示

n个圆盘互不相交,n个圆盘均在右半平面即不包含原点。
所以A有个n个互不相同的实特征值,故A可逆且可相似对角化。


