数量关系

数量关系
- 数的性质
- 数列规律
  - 做差法
  - 做商法
  - 乘积法
  - 求和法
  - 指数法
  - 分解法
- 年龄问题
- 行程问题
- 利润问题
  - 定价曲线
  - 打折出售
- 工程问题
- 概率问题
  - 乘法
  - 排列
  - 组合
  - 组排
  - 捆绑
  - 插空
  - 挡板
  - 古典
  - 重复
- 浓度问题
- 容斥问题
- 抽屉问题
- 鸡兔同笼
- 吃草问题
- 方阵问题
- 植树问题
- 时钟问题
- 最值问题
- 几何问题

数的性质

奇偶

加减
- 奇和为偶：奇 + 奇 = 偶
- 奇偶和奇：奇 + 偶 = 奇、偶 + 奇 = 奇
- 和差同性：M + N与M - N的奇偶同性
- 同和为偶：X + X = 偶
相乘
- 有偶为偶：奇 × 奇 × ... × 偶 = 偶
- 全奇为奇：奇 × 奇 × ... × 奇 = 奇

例：77个蛋糕，大盒能装15个，小盒能装8个，要求恰好装满，问需要几个盒子。

$77 = 15x + 8y$ ，因为 $77$ 为奇数、 $8y$ 为偶数，
所以 $15x$ 一定为奇数，即 $x$ 一定为奇数。
$x$ 在 $1,3,5$ 中尝试，得 $x=3$ ， $y=4$ ， $x+y=7$ 。

整除

若 $a$ 能被 $b$ 整除，则 $a ~mod~ b = 0$ 。

数字	方法	例子
2	个位是否能被2整除	122、254
5	个位是否能被5整除	255、395
4	末2位是否能被4整除	812、724、636
25	末2位是否能被25整除	725、825
3	各位数字和能否被3整除	156（`1+5+6=9`）
9	各位数字和能否被9整除	675（`6+7+5=18`）
7	个位2倍与剩下数之差能被7整除或末3位与剩下数之差能被7整除	392（`4-39=-35`） 8442（`442-8=434`、`8-43=35`）
11	`奇数位和-偶数位和`能被11整除或末3位与剩下数之差能被11整除	9658（`658-9=649`、`6+9-4=11`） 15235（`235-15=220`、`2+0-2=0`）
13	末3位与剩下数之差能被13整除	1274（`274-1=273=260+13`）

补充性质：

整除传递： $\{a ~mod~ b = 0 ~\&\&~ b ~mod~ c = 0\} ~⇒~ \{a ~mod~ c = 0\}$
同子和差： $\{a ~mod~ c = 0 ~\&\&~ b ~mod~ c = 0\} ~⇒~ \{(a+b) ~mod~ c = 0 ~\&\&~ (a-b) ~mod~ c = 0\}$
倍父同效： $\{a ~mod~ c = 0 ~\&\&~ n∈N\} ~⇒~ \{na ~mod~ c = 0\}$
同堂互质： $\{a ~mod~ b = 0 ~\&\&~ a ~mod~ c = 0 ~\&\&~ a,b互质\} ~⇒~ \{a ~mod~ bc = 0\}$

同余

若 $\{a ~mod~ c = b ~mod~ c\}$ ，则称 $a$ 、 $b$ 对于 $c$ 同余。

设 $a=xc+v$ $a = x c + v$ 、 $b=yc+w$ $b = yc + w$
- $(a+b)~mod~c = (v+w)~mod~c$
- $(a-b)~mod~c = (v-w)~mod~c$
- $(a \cdot b)~mod~c = (v \cdot w)~mod~c$

例1：求 $2011×2012$ 的余数

$2011×2012~mod~6 = (2011~mod~6)×(2012~mod~6) = (1×2)~mod~6 = 2$

例2：一个整数除 $x,y,z$ 的余数都为 $r$ ，求这个整数。

余同加余：(x, y, z)的最小公倍数 + r

例3：一个整数除 $x,y,z$ 的余数分别为 $(r-x),(r-y),(r-z)$ ，求这个整数。

和同加和：(x, y, z)的最小公倍数 + r

例4：一个整数除 $x,y,z$ 的余数分别为 $(x-r),(y-r),(z-r)$ ，求这个整数。

差同加差：(x, y, z)的最小公倍数 + r

求最大公因数

互质：若 $a$ 、 $b$ 的最大公因数为 $1$ ，则称 $a$ 、 $b$ 互质。

求解方法：质因数分解。

求最小公倍数

求解方法：先求最大公因数、再将两边剩余因数相乘、最后乘以最大公因数。

例1：求 $24$ 与 $36$ 的最小公倍数

$24 = 2 × 12$ 、 $36 = 3 × 12$

$2 × 3 × 12 = 72$

例2：已知 $\begin{cases} 60 = x_1 + x_2 + y_1 + y_2 + z \\ 4(x_2+y_2) = (x_1+y_1) \\ (y_1+y_2) = 7(x_1+x_2) \end{cases}$ ，问 $z=?$ （变量全为整数）

$A.12 ~~ B.15 ~~ C.20 ~~ D.25$

$\begin{cases} (x_2 + y_2) = \dfrac{60 - z}{5} \\ (x_1 + x_2) = \dfrac{60 - z}{8} \end{cases}$

即 $(60-z)$ 为 $5$ 和 $8$ 的最小公倍数，即为 $40$ ，故 $z=20$

和差倍比

和倍关系：已知 $s=(a+b)$ 、 $p=\dfrac{a}{b}$ ，则 $b=\dfrac{s}{p+1}$
和差关系：已知 $s=(a+b)$ 、 $d=(a-b)$ ，则 $a=\dfrac{s+d}{2}$

例1：三人生肖相同，年龄和为72，则年龄最小的人今年不可能为：

$A.6 ~~ B.8 ~~ C.12 ~~ D.16$

设最小的人年龄为 $x$ ，其它两人分别为 $(x+a)$ 、 $(x+b)$ ，则有

$72 = x + (x+a) + (x+b)$ ，即 $(a+b) = 72 - 3x$

三人生肖相同，故 $(a+b)$ 一定为 $12$ 的整数倍

故 $3x$ 也一定为 $12$ 的整数倍，即 $x$ 为4的整数倍

综上答案为 $A$

数列规律

①前两项与后一项（可能有间隔）的关系（ $a_{i+1} = a_{i} ~?~ a_{i-1}$ ）
②位置信息代入什么公式（线性 $+i,×i$ 、指数 $+i^n,×i^n$ ）
③数本身是否已经包含位置信息（ $a_i = i × ~?~$ ）

做差法

例：1, 2, 4, 7, 11, ( ), ( )。

作差：1, 2, 3, 4, (5), (6)
结果：1, 2, 4, 7, 11, (16), (22)

做商法

例：3, 6, 18, 72, 360, ( )。

做商：2, 3, 4, 5, (6)
结果：3, 6, 18, 72, 360, (2160)

乘积法

例：1, 2, 3, 8, 27, 220, ( )。

作积：1×2+1=3, 2×3+2=8, 3×8+3=27, 8×27+4=220, 27×220+5=(5945)

求和法

例：1, 2, 3, 5, 8, 13, 21, ( )。

作和：1+2=3, 2+3=5, 5+8=13, 8+13=21, 13+21=(34)

指数法

$i^2: {0,1,4,9,16,25,\cdots}$
$i^2-i: {0,0,2,6,12,20,\cdots}$
$i^3: {0,1,8,27,64,125,\cdots}$
$i^3-i: {0,0,6,24,60,120,\cdots}$

例：0, 0, 6, 24, 60, 120, ()。

指数：0**3-0=0, 1**3-1=0, 2**3-2=6, 3**3-3=24, 4**3-4=60, 5**3-5=120, 6**3-6=(210)

分解法

例：3, 8, 15, 24, ( )。

分解：1×2+1=3, 2×3+2=8, 3×4+3=15, 4×5+4=24, 5×6+5=(35)

年龄问题

解题思路：某时间段年龄 $x$ 、 $y$ ，关系为 $f(x,y)$ ， $n$ 年后关系 $g(x+n,y+n)$ ，则有

$\begin{cases} f(x,y) \\ g(x+n,y+n) \end{cases}$

例： $3$ 年前A是B的年龄的 $17$ 倍， $3$ 年后，A是B的年龄的 $5$ 倍，问B现在多少岁。

设3年前A、B年龄分别为 $x$ 、 $y$ ，则有：

$\begin{cases} x = y × 17 \\ (x+6) = (y+6) × 5 \end{cases}$

解得 $x=34$ 、 $y=2$

行程问题

火车问题

火车过桥：速度 × 时间 = 车长 + 桥长

火车相遇：相遇时间 × (甲车速 + 乙车速) = 甲车长 + 乙车长 + 甲乙距离

火车追及：追及时间 × (甲车速 - 乙车速) = 甲车长 + 乙车长 + 甲乙距离

例：一列火车长150米，速度19m/s。全车通过长800米的大桥，需要多少时间

$t = \dfrac{150 + 800}{19} = 50s$

流水问题

解题思路：(船速 + 水速) × 顺行时间 = (船速 - 水速) × 逆行时间

例：甲船从A地航行到下游需要 $6$ 小时，由B地航行到A地需要 $12$ 小时，乙船在静水中的速度是甲船的 $3$ 倍，问乙从B航行到A需要多长时间。

设两地距离为 $L$ ，水速为 $s$ ，甲船速度为 $v$ ，则有：

$\begin{cases} L = (v+s)6 = (v-s)12 ~⇒~ v=3s,L=24s \\ \dfrac{L}{3v-s} = \dfrac{24s}{9s-s} = 3 \end{cases}$

相遇问题

相向相遇：两地距离 = 相遇耗时 × (甲速度 + 乙速度)

快返相遇：2 × 两地距离 = 相遇耗时 × (甲速度 + 乙速度)

同地多次相遇：两人总移动距离 = 两地距离 × (2 × 相遇次数)

异地多次相遇：两人总移动距离 = 两地距离 × (2 × 相遇次数 - 1)

同地环型相遇：两人总移动距离 = 第一次相遇两者移动距离 × 相遇次数

遛狗问题

$A$ 、 $B$ 从相距 $L$ 的两地相向而行， $C$ 随 $A$ 一起出发在 $A$ 与 $B$ 之间来回奔跑，三者速度分别为 $v_a$ 、 $v_b$ 、 $v_c$ （ $v_c > v_a$ ），问当 $A$ 与 $B$ 相遇时， $C$ 跑的路程 $s_c$ 为多远？

$L = t × (v_a + v_b)$
$s_c = t × v_c$

利润问题

解题思路1：利润 = 售价 × 打折系数 - 成本 = 利润率 × 成本

解题思路2：售价 × 打折系数 = (1 + 利润率) × 成本

定价曲线

例1：定价3000元时，能售出15万件，定价每增加200元，少出售1万件，若实际仅售出12万件，则销售策略为？

定价： $3000 + 200 × \dfrac{15w - 12w}{1w} = 3600$

打折出售

例1：进价800，标价1440，希望打折后利润率不低于35%，最低可以打几折？

$\dfrac{1440×x-800}{800} ≥ 0.35 ~⇒~ x≥0.75$

例2：八折销售，利润为进价的 $60\%$ ，打七折，利润为50，求原价？

$\begin{cases} 0.8p - c = 0.6c \\ 0.7p - c = 50 \end{cases} ~⇒~ p=2c=250$

工程问题

解题思路：工作量 = 工作效率 × 时间，完成单个任务所耗费的时间的倒数即为工作效率。

剩余工作

解题思路：(全部工作量 - 已完成工作量) = 新工作效率 × 剩余时间

例：14台收割机收完麦子需要20天，收割了2天后，增加了6台，并改造使效率提升5%，问还需要几天收完？

设初始每台每天工作效率为 $e$

$t = \dfrac{14e × 20 - 14e × 2}{20e × (1+5\%)} = 12$

提前完成

$t_1=\frac{q}{e}$ 、 $t_2=\frac{q}{e(1+p)}=\frac{q}{e}\cdot\frac{1}{1+p}$ 、 $t_1-t_2=\frac{q}{e}\cdot\frac{p}{1+p}$

$\frac{t_1}{t_1-t_2} = \frac{1+p}{p}$ （提效倍比）

解题思路：原效率总时间 = 提前时间 × 提效倍比、工作量 = 提前时间 × 提效倍比 × 原效率

例1：计划植树300棵，实际效率为原效率1.2倍，结果提前20分钟完成，求原效率（棵/小时）？

$e = \dfrac{300}{\frac{1}{3} × \frac{1.2}{0.2}} = 150$

例2：种树，每天多种 $\frac{1}{4}$ 提前 $9$ 天完成，种了 $4000$ 棵后每天多种 $\frac{1}{3}$ 提前 $5$ 天完成，共有多少树？

$\begin{cases} q = 9 × \frac{1 + 1/4}{1/4} × e \\ (q-4000) = 5 × \frac{1 + 1/3}{1/3} × e \end{cases} ~⇒~ e=160, q=7200$

合作工程

$\frac{q}{xe} - \frac{q}{ye} = Δt ~⇒~ q = \frac{Δt}{\frac{1}{x} - \frac{1}{y}}e$

解题思路1：总工作量 = 所有人工作效率和 × 总工作时间

解题思路2：总工作量 = (不同效率时间差/效率倒数差) × 单位效率

例1：修2个隧道（900米、1250米），A、B、C队效率分别为24、30、32米/天，A队修1隧道，C队修2隧道，B队先修1后修2，两地同时完工，B修了几天1隧道？

$900 + 1250 = (24 + 30 + 32)t ~⇒~ t=25$

或

$\begin{cases} 900 = 24t + 30t_0 \\ 1250 = 32t + 30(t-t_0) \end{cases} ~⇒~ t=25,t_0=10$

例2：3名绣工8天可完成，完成50%时一人离开，完成75%时又一人离开，最后实际用了几天。

$q = 3e × 8 = 24e$

$\dfrac{\frac{1}{2}×24e}{3e} + \dfrac{\frac{1}{4}×24e}{2e} + \dfrac{\frac{1}{4}×24e}{e} = 13$

例3：四人合作效率比为 $3:5:4:6$ ，前2个合作比后2个合作多9天，问4人合作共需要多少天？

$q = \dfrac{9}{\frac{1}{8}-\frac{1}{10}} = 360e$

$\dfrac{360e}{18e} = 20$

例4：甲单独16小时，乙单独12小时，甲乙交替每次1小时，问需要多久？

由完成时间比得甲乙效率比为 $3:4$ （时间的反比）

$q = \dfrac{16-12}{\frac{1}{3}-\frac{1}{4}} = 48e$

$\dfrac{48e}{7e} = 6...6e$

$\dfrac{6e}{3e} = 1...3e$

$\dfrac{3e}{4e} = 0.75$

$t = 6 × 2 + 1 + 0.75 = 13.75$

放水问题

$q=t_1e_1=t_2e_2$ 、 $\frac{q}{e_1-e_2}=\frac{q}{\frac{q}{t_1}-\frac{q}{t_2}}=\frac{t_1t_2}{t_2-t_1}$

解题思路：消耗时间 = 时间积/时间差

例：A口入水，灌满需要2h；B口出水，满池放空需要1.5h；现有1/3水，同时打开AB口，排空需要多久？

$t = \dfrac{1}{3} \cdot \dfrac{1.5 × 2}{2 - 1.5} = 2$

概率问题

排列数： $A_n^m = \dfrac{n!}{(n-m)!}$
全排列： $A_n^n = n!$
组合数： $C_n^m = \dfrac{A_n^m}{m!} = \dfrac{1}{m!} \cdot \dfrac{n!}{(n-m)!}$
条件概率： $A$ 在 $B$ 发生的条件下发生的概率为， $P(A|B)=\dfrac{P(AB)}{P(B)}$
独立重复实验：每次 $A$ 发生的概率为 $p$ ，在 $n$ 次实验中 $A$ 发生 $k$ 次的概率为， $P(A_k) = C_n^kp^k(1-p)^{n-k}$

乘法

例1：4个信箱，5封信，有几种投法？

每封信有4个选择，共有 $4^5=1024$ 种。

例2：7×7队列，随机选中一个，再选中一个不再同行同列的，有几种选法。

$(7×7) × (6×6) = 1764$

排列

例1：10个人，选4个排一列，几种排法？

$A_{10}^4 = 7×8×9×10 = 5040$

组合

例1：8个人，选4个培训，2个培训计算机，1个培训英语，1个培训财务，有几种人选方法？

$C_{8}^{2} C_{6}^{1} C_{5}^{1} = 28×6×5 = 840$

组排

例1：5男，5女，选4人，每人表演1个节目，要求4人有男有女，不能由男生连续表演。

①、1男3女： $(C_5^1 C_5^3) A_4^4 = 1200$
②、2男2女： $(C_5^2 C_5^2) A_2^2 A_3^2 = 1200$
③、3男1女：不满足连续表演要求
综上： $1200 + 1200 = 2400$

捆绑

例1：3组老年夫妇看电影坐一排（6个位置），同一家庭必须坐一起，有几种坐法？

$A_3^3×(A_2^2)^3 = 48$

例2：拔河比赛，3男3女，3男不能全部连在一起，有几种不同的站位？

3男看成整体， $A_6^6 - A_4^4×A_3^3 = 576$

插空

例1：两部门分别排3个，2个节目，要求不能连续出场，有几种排法？

$A_3^3 × A_2^2 = 12$

例2：12棵松树，6棵柏树，种道路两侧，两侧树种数量相同，要求道路起始必为松树，柏树不能相邻，有几种种法？

每侧6棵松树，5个空， $(C_5^3)^2 = 100$

挡板

例1：7个橘子分给4个小朋友，每人至少一个，有几种分配方法？

7个橘子6个空，4个小朋友3个挡板， $C_6^3 = 20$

例2：10个名额分到 $n$ 个科室，每个科室至少一个名额，有36种分配方法，求 $n$ ？

$(n-1)$ 个空， $(10-1)$ 个挡板， $C_{10-1}^{n-1} = 36 ~⇒~ n=3,8$

古典

例1：5男，3女，选2人，正好1男1女的概率

$\dfrac{C_5^1 C_3^1}{C_8^2} = \dfrac{15}{28}$

重复

例1：每次命中 $10$ 环概率为 $\dfrac{2}{3}$ ， $5$ 次射击共 $3$ 次命中的概率是多少？

$C_5^3 (\dfrac{2}{3})^3 (\dfrac{1}{3})^2 = \dfrac{80}{243}$

浓度问题

解题思路：溶质质量 = 浓度 × 溶液体积

例：1份甲和2份乙混合后浓度为22%，3份乙和4份丙合并后为35%，1份甲和1份丙合并后为43%，问甲乙丙5：4：1合并后的浓度？

设每份溶液甲乙丙的溶质量分布为 $x$ 、 $y$ 、 $z$

$\begin{cases} 3 × 0.22 = x + 2y \\ 7 × 0.35 = 3y + 4z \\ 2 × 0.43 = x + z \end{cases} ~⇒~ x=0.36,y=0.15,z=0.50$

$\dfrac{5x+4y+z}{10} = 29\%$

容斥问题

两个集合

A∪B = (A + B) - AnB
二个全中 = AnB
仅有一个 = A∪B - AnB
全部情况 = A∪B + 不在AB的剩余部分

两个集合全集

AnB = (A + B) - 1

三个集合

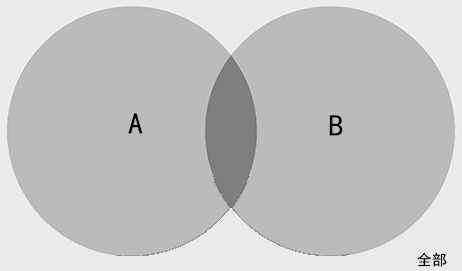
A∪B∪C = (A + B + C) - (AnB + AnC + BnC) + AnBnC
三个全中 = AnBnC
仅有二个 = (AnB + AnC + BnC) - 3 × AnBnC
全部情况 = A∪B∪C + 不在ABC的剩余部分

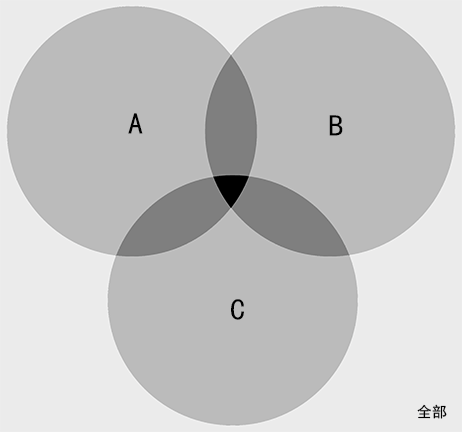
例：使用太阳能热水器36人，选乘公共交通工具上下班21人，自备购物袋47人。三个均为肯定的有4人，仅有2个肯定的有46人，3个均否定的有15人，问总调查人数？

$AnBnC = 4$

$(AnB + AnC + BnC) - 3 × AnBnC = 46 ~⇒~ (AnB + AnC + BnC) = 58$

$(A + B + C) = 36 + 21 + 47 = 104$

$全部情况 = 104 - 58 + 4 + 15 = 65$

抽屉问题

解题思路： $R=(r-1)n + 1$

例：5个抽屉和若干苹果，至少保证有一个抽屉有4个苹果，则是少有多少个苹果？

$(4-1) × 5 + 1 = 16$

鸡兔同笼

解题思路：头 = 鸡 + 兔、脚 = 2 × 鸡 + 4 × 兔

吃草问题

解题思路：天数 × 每天生长 + 最初草量 = 每牛每日量 × 头数 × 天数 ⇒ 最初草量 = (每牛每日量 × 头数 - 每天生长) × 天数

例：草地可供10牛吃20天，15牛吃10天，问可供25牛吃几天？

设每牛每天吃 $m$ ，初草量为 $q$ ，每天新增草为 $n$ ，可供25牛吃 $x$ 天：

$\begin{cases} q = (10m - n) × 20 \\ q = (15m - n) × 10 \\ q = (25m - n) x \end{cases} ~⇒~ n=5m, q=100m, x=5$

方阵问题

性质：

相邻两层人数差8
实心方阵总人数 = 最外层每边人数 ** 2
每层人数 = 该层每边人数 × 4 - 4
去掉 $n$ 行 $n$ 列：去掉人数 = 原每行人数 × 2n - n × n

植树问题

性质：

闭区间：棵树 = 路长 ÷ 间距 + 1
半开半闭/环型：棵树 = 路长 ÷ 间距
开区间：棵树 = 路长 ÷ 间距 - 1

时钟问题

弧长 = 半径 × 弧度

时针每分钟走 $\frac{5}{60}=\frac{1}{12}$ 格、 $0.5°$ 、 $\frac{\pi}{360}$

分针每分钟走 $1$ 格、 $6°$ 、 $\frac{\pi}{30}$

分针 = 时针 × 12

例1：时针分钟重合时出发，时针转30°后返回，此时分钟转过的角度为？

$\dfrac{x}{30} = \dfrac{6}{0.5} ~⇒~ x=360$

最值问题

$ax^2 + bx + c = 0$

对称轴： $-\dfrac{b}{2a}$

$Δ = b^2 - 4ac$

$Δ < 0$ ，没有解

$Δ = 0$ ， $x_1 = x_2$

$Δ > 0$ ，两个解

$x = \dfrac{-b ± Δ}{2a}$

几何问题

略